Question

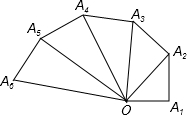第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的．且OA₁=A₁A₂=A₂A₃=A₃A₄=…=A₉A₁₀=1．如果把图中的直角三角形继续画下去，那么
（1）线段OA₂=

 

，线段OA₄=

 

；
（2）线段OA₁，OA₂，OA₃，OA₄，…，OA₁₀中，有

 

条线段的长度为无理数．

Answer 1

考点：勾股定理,无理数

专题：规律型

分析：（1）利用勾股定理即可求出线段OA₂和线段OA₄的长度；
（2）根据勾股定理分别计算出线段OA₁，OA₂，OA₃，OA₄，…，OA₁₀即可得到线段的长度为无理数．

解答：解：（1）由勾股定理可得：线段OA₂=

12+12

=

2

，线段OA₄=

3+1

=2；
故答案为：

2

，2．
（2）由勾股定理可得线段OA₁，OA₂，OA₃，OA₄，…，OA₁₀的长度，有7条线段的长度为无理数．
故答案为：7．

点评：本题考查了勾股定理的运用，解题的关键是反复利用勾股定理，依次递进，逐步求出每个斜边的长．