题目内容
 如图,三角形ABC中,∠A=75°,∠B=35°,B,C,D三点在同一直线上,CD∥AB,求三角形ABC内角和的度数.
如图,三角形ABC中,∠A=75°,∠B=35°,B,C,D三点在同一直线上,CD∥AB,求三角形ABC内角和的度数.考点:三角形内角和定理,平行线的性质
专题:计算题
分析:根据平行线的性质得∠ACD=∠A=35°,∠ECD=∠B=75°,再利用平角的定义得到∠ACB+∠ACD+∠ECD=180°,所以∠ACB+∠A+∠B=180°.
解答:解:∵CD∥AB,
∴∠ACD=∠A=35°,∠ECD=∠B=75°,
又∵B,C,D三点在同一条直线上,
∴∠ACB+∠ACD+∠ECD=180°,
∴∠ACB+∠A+∠B=180°,
即三角形ABC内角和的度数是180°.
∴∠ACD=∠A=35°,∠ECD=∠B=75°,
又∵B,C,D三点在同一条直线上,
∴∠ACB+∠ACD+∠ECD=180°,
∴∠ACB+∠A+∠B=180°,
即三角形ABC内角和的度数是180°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了平行线的性质.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
甲数的2倍比乙数大3,甲数的3倍比乙数的2倍小1,若设甲数为x,乙数为y,则根据题意可列出的方程组为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
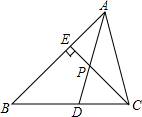 如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数. 如图,点E、P在?ABCD的对角线BD所在直线上,且点E、F分别在BD的两侧,
如图,点E、P在?ABCD的对角线BD所在直线上,且点E、F分别在BD的两侧, 画图并填空:
画图并填空: 请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为1,
请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为1,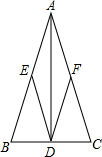 如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点.
如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点. 如图,已知AB∥CD,直线EF分别交直线AB,CD于点E、F,FG平分∠CFE交AB于点G,若∠BEF=70°,求∠AGF的度数.
如图,已知AB∥CD,直线EF分别交直线AB,CD于点E、F,FG平分∠CFE交AB于点G,若∠BEF=70°,求∠AGF的度数. (1)如图,已知△ABC,试画出AB边上的中线和AC边上的高;
(1)如图,已知△ABC,试画出AB边上的中线和AC边上的高;