题目内容
3.如图1,正方形ABCD中,点P从点A出发,以每秒2厘米的速度,沿A→D→C方向运动,点Q从点B出发,以每秒1厘米的速度,沿BA向点A运动,P、Q同时出发,当点P运动到点C时,两动点停止运动,若△PAQ的面积y(cm2)与运动时间x(s)之间的函数图象为图2,若线段PQ将正方形分成面积相等的两部分,则x的值为6.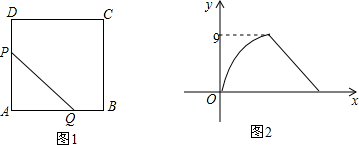
分析 由题意可知,由图象可知当点P运动至点D重合时,△PAQ的面积最大,此时点Q位于AB的中点,即AQ=$\frac{a}{2}$,根据面积的最大值求得正方形的边长,PQ要平分正方形面积,必过中心,此时CP=12-2t,AQ=6-t,需要满足CP=AQ,据此可得.
解答 解:设正方形的边长为acm,
由图象可知当点P运动至点D重合时,△PAQ的面积最大,此时点Q位于AB的中点,即AQ=$\frac{a}{2}$,
则$\frac{1}{2}$•a•$\frac{a}{2}$=9,
解得:a=6或a=-6(舍),
∵PQ平分正方形面积,
∴PQ必过正方形的中心,此时CP=12-2t,AQ=6-t,
由CP=AQ可得12-2t=6-t,
解得:t=6,
故答案为:6.
点评 本题主要考查动点问题的函数图象,结合题意分析点的运动轨迹,并列出函数关系式是关键,结合函数关系式及性质求某一时刻的值则是基本运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在四个实数$\frac{3}{2}$,0,-1,$\sqrt{3}$中,最大的是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | -1 | D. | $\sqrt{3}$ |
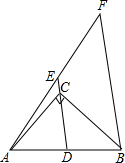 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.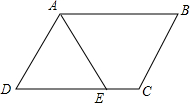 如图,在?ABCD中,AB>BC,AE平分∠BAD交CD于点E,如果?ABCD的周长为20,EC=2,求AB、BC的长.
如图,在?ABCD中,AB>BC,AE平分∠BAD交CD于点E,如果?ABCD的周长为20,EC=2,求AB、BC的长.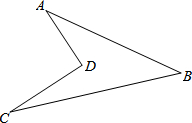 如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.
如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.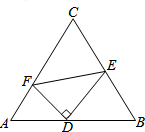 如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为1.5.
如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为1.5.