题目内容
8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:①AD是∠BAC的平分线;②∠ADB=120°;③AD=BD;④DB=2CD.
其中正确的结论共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据角平分线的作法可得①正确;再根据三角形内角和定理和外角与内角的关系可得∠ADB=120°,可得②正确;再根据等角对等边可得③正确;根据直角三角形中30°角所对的直角边等于斜边的一半可得④正确.
解答  解:①AD是∠BAC的平分线,结论正确;
解:①AD是∠BAC的平分线,结论正确;
②∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠DAC=∠DAB=30°,
∴∠ADB=∠DAC+∠C=30°+90°=120°,结论正确;
③∵∠DAB=30°,∠B=30°,
∴AD=BD,结论正确,
④∵∠C=90°,∠CAD=30°,
∴AD=2CD,
由③知AD=BD,
∴DB=2CD,结论正确.
故选:A.
点评 此题主要考查了角平分线的作法,三角形内角和定理,外角的性质,含30度角的直角三角形的性质,根据角平分线的作法得出AD是∠BAC的平分线是解题的关键.

练习册系列答案
相关题目
16.在下列长度的四根木棒中,能与5cm,11cm长的两根木棒首尾相接,钉成一个三角形的是( )
| A. | 5cm | B. | 6cm | C. | 11cm | D. | 16cm |
 已知:如图,在△ABC中,点A(-3,2),B(-1,1).
已知:如图,在△ABC中,点A(-3,2),B(-1,1).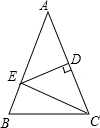 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.求∠ECB的度数.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.求∠ECB的度数.