题目内容
15.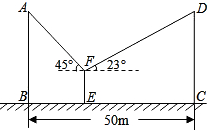 已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
分析 过点F作AB、CD的垂线,垂足为点G、H,设AG=DH=x,由$\frac{AG}{tan45°}$+$\frac{AG}{tan23°}$=BC,解得AG的值,则根据AB=AG+FE即可求出电线杆的高度.
解答 解:过点F作AB、CD的垂线,垂足为点G、H.
设AG=xm,则有DH=xm.
$\frac{AG}{tan45°}$+$\frac{AG}{tan23°}$=BC,
∴tan23°=$\frac{x}{50-x}$,
解得:x≈15.0,
∴AB=x+1.5=16.5.
答:电线杆的高度约为16.5m.
故答案为:16.5.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
20.2014年12月12日南水北调中线工程正式通水,每年可向北方输送95亿立方米的水量,95亿用科学记数法表示为( )
| A. | 9.5×107 | B. | 9.5×108 | C. | 9.5×109 | D. | 9.5×1010 |
7.一组数据4,3,6,9,6,5的极差和众数分别是( )
| A. | 5和5.5 | B. | 5.5和6 | C. | 5和6 | D. | 6和6 |
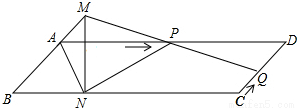 已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)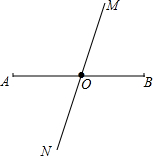 如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小.
如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小. 如图,AB与CD相交于点O,若∠COB:∠BOD=5:1,则∠AOD=150°,∠AOC=30°.
如图,AB与CD相交于点O,若∠COB:∠BOD=5:1,则∠AOD=150°,∠AOC=30°.