题目内容
10. 如图,矩形OABC的边OA,OC分别在x轴,y轴上,D为BC上一点,DE⊥OD交AB于E,OD=DE,双曲线y=$\frac{1}{x}$(x>0)经过D,E两点,求OA2-AE2的值.
如图,矩形OABC的边OA,OC分别在x轴,y轴上,D为BC上一点,DE⊥OD交AB于E,OD=DE,双曲线y=$\frac{1}{x}$(x>0)经过D,E两点,求OA2-AE2的值.
分析 设出D(m,n),然后根据已知证得△OCD≌△DBE(AAS),得出OC=BD,CD=BE,从而得出E(m+n,n-m),即可得出OA=m+n,AE=n-m,然后根据OA2-AE2=(OA+AE)(OA-AE)以及k=xy求得即可.
解答 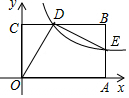 解:∵DE⊥OD,
解:∵DE⊥OD,
∴∠ODE=90°,
∴∠ODC+∠EDB=90°,
∵∠ODC+∠COD=90°,
∴∠EDB=∠COD,
在△OCD和△DBE中
$\left\{\begin{array}{l}{∠EDB=∠COD}\\{∠OCD=∠B}\\{OD=DE}\end{array}\right.$
∴△OCD≌△DBE(AAS),
∴OC=BD,CD=BE,
设D(m,n),则E(m+n,n-m),
∴OA=m+n,AE=n-m,
∵双曲线y=$\frac{1}{x}$(x>0)经过D,E两点,
∴mn=1,
∴OA2-AE2=(OA+AE)(OA-AE)=(m+n+n-m)(m+n-n+m)=2n•2m=4mn=4.
点评 本题考查了反比例函数图象上点的坐标特征,矩形的性质以及三角形全等的判定和性质,得出E的坐标是解题的关键.

练习册系列答案
相关题目
20.一个底面是正方形的水池,容积是11.52m3,池深2m,则水池每边边长是( )
| A. | 9.25m | B. | 13.52m | C. | 2.4m | D. | 4.2m |
15.一元二次方程x2-10x+21=0的解是( )
| A. | -7 | B. | 3 | C. | 7或3 | D. | -7或3 |
19.下列四组线段中,可以构成直角三角形的是 ( )
| A. | 1、2、3 | B. | 3、4、5 | C. | 1、1、$\sqrt{3}$ | D. | 6、7、8 |
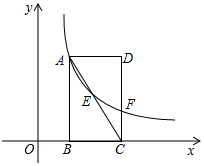 如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3). 在平面直角坐标系中,描出下列各点A(2,1),B(6,1),C(3,5),D(7,5),并将各点用线段依次连接起来,观察得到的图形是平行四边形?并说明理由.
在平面直角坐标系中,描出下列各点A(2,1),B(6,1),C(3,5),D(7,5),并将各点用线段依次连接起来,观察得到的图形是平行四边形?并说明理由.