题目内容
 连接边长为1的正方形对边中点,可将一个正方形分成2个大小相同的长方形,选右边的长方形进行第二次操作,又可将这个长方形分成2个更小的正方形…重复这样的操作,经过仔细地观察与思考,猜想
连接边长为1的正方形对边中点,可将一个正方形分成2个大小相同的长方形,选右边的长方形进行第二次操作,又可将这个长方形分成2个更小的正方形…重复这样的操作,经过仔细地观察与思考,猜想| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-(
)n.
| 1 |
| 2 |
1-(
)n.
.| 1 |
| 2 |
分析:由图中可知:
+(
)2=1-(
)2;
+(
)2+(
)3=1-(
)3;…,故左侧式子的和等于1减去最后一个加数,据此求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:根据题意可得,
=1-
;
+(
)2=1-(
)2;
+(
)2+(
)3=1-(
)3;
…
故
+(
)2+(
)3+…+(
)n-1+(
)n=1-(
)n.
故答案为:1-(
)n.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
…
故
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:1-(
| 1 |
| 2 |
点评:本题考查了图形的变化类问题,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
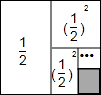 连接边长为1的正方形对边中点,可将一个正方形分成2个大小相同的长方形,选右边的长方形进行第二次操作,又可将这个长方形分成2个更小的正方形…重复这样的操作,经过仔细地观察与思考,猜想
连接边长为1的正方形对边中点,可将一个正方形分成2个大小相同的长方形,选右边的长方形进行第二次操作,又可将这个长方形分成2个更小的正方形…重复这样的操作,经过仔细地观察与思考,猜想 4、如图所示,连接边长为1的正方形各边的中点,连接正方形的对角线,则图中共有三角形( )
4、如图所示,连接边长为1的正方形各边的中点,连接正方形的对角线,则图中共有三角形( ) 如图,连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2011次操作后右下角的小正方形面积是 ( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2011次操作后右下角的小正方形面积是 ( ) 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2004次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2004次操作后右下角的小正方形面积是( )