题目内容
 在矩形ABCD中,AB=3,BC=6,BE=2EC,DM⊥AE于点M,求DM.
在矩形ABCD中,AB=3,BC=6,BE=2EC,DM⊥AE于点M,求DM.考点:矩形的性质
专题:
分析:连接DE,求出BE的长度,利用勾股定理列式求出AE,然后利用△ADE的面积列方程求解即可.
解答: 解:如图,连接DE,
解:如图,连接DE,
∵BC=6,BE=2EC,
∴BE=
×6=4,
在Rt△ABE中,由勾股定理得,AE=
=
=5,
∵DM⊥AE,
∴S△ADE=
AE•DM=
AD•AB,
即
×5•DM=
×6×3,
解得DM=
.
 解:如图,连接DE,
解:如图,连接DE,∵BC=6,BE=2EC,
∴BE=
| 2 |
| 1+2 |
在Rt△ABE中,由勾股定理得,AE=
| AB2+BE2 |
| 32+42 |
∵DM⊥AE,
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得DM=
| 18 |
| 5 |
点评:本题考查了矩形的性质,勾股定理,熟记性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
相关题目
在实数:3.14159,
,1.010010001…,
,4.
,
,
中,无理数有( )
| 3 | 64 |
| 8 |
| •• |
| 21 |
| π |
| 3 |
| 22 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列选项中的算式,其计算结果是负数的是( )
| A、(-1)×(+2)×0 |
| B、(-0.5)÷(-1.84) |
| C、(-5)+(-6) |
| D、-1+1 |
 如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少?
如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少? 如图,⊙O1和⊙O2内切,它们的半径分别为r1=2cm,r2=5cm,连心线与⊙O1交于A、B,与⊙O2交于点A、C,求线段BC的长.
如图,⊙O1和⊙O2内切,它们的半径分别为r1=2cm,r2=5cm,连心线与⊙O1交于A、B,与⊙O2交于点A、C,求线段BC的长. 如图,已知过P点的直线与⊙O相交于A、B,AB为⊙O的直径,PC为⊙O的切线,C为切点,BD⊥PC于D,交圆心O于点E,∠P=30°,AB=2,求DE的长.
如图,已知过P点的直线与⊙O相交于A、B,AB为⊙O的直径,PC为⊙O的切线,C为切点,BD⊥PC于D,交圆心O于点E,∠P=30°,AB=2,求DE的长.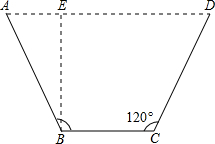 用一块宽度为5m的矩形铁皮弯折成如图所示的等腰梯形流水槽,要使流水槽的横截面面积最大,弯折的长度(梯形的腰)应为多少?
用一块宽度为5m的矩形铁皮弯折成如图所示的等腰梯形流水槽,要使流水槽的横截面面积最大,弯折的长度(梯形的腰)应为多少?