题目内容
 如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少?
如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少?考点:相似三角形的判定与性质,梯形
专题:
分析:先根据AD∥BC,BC∥EF得出AD∥BC∥EF,故△AOE∽△ACB,△BOE∽△BDA,△DOF∽△DBC,△COF∽△CAD,再由相似三角形的对应边成比例即可得出结论.
解答:解:∵AD∥BC,BC∥EF,
∴AD∥BC∥EF,
∴△AOE∽△ACB,△BOE∽△BDA,△DOF∽△DBC,△COF∽△CAD,
∴
=
①,
=
②,
=
③,
=
④,
∴①+②得,
+
=1⑤,③+④得,
+
=1⑥,
∴⑤+⑥得,
+
=2,
∵EF=36,AD=24,
∴
+
=2,
解得BC=72cm.
∴AD∥BC∥EF,
∴△AOE∽△ACB,△BOE∽△BDA,△DOF∽△DBC,△COF∽△CAD,
∴
| OE |
| BC |
| AE |
| AB |
| OE |
| AD |
| BE |
| AB |
| OF |
| BC |
| DF |
| AB |
| OF |
| AD |
| CF |
| DC |
∴①+②得,
| OE |
| BC |
| OE |
| AD |
| OF |
| BC |
| OF |
| AD |
∴⑤+⑥得,
| EF |
| BC |
| EF |
| AD |
∵EF=36,AD=24,
∴
| 36 |
| BC |
| 36 |
| 24 |
解得BC=72cm.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中根据相似三角形对应边比例相等性质解答是解题的关键.

练习册系列答案
相关题目
若-2x+1=5y-2,则10y-(1-4x)的值是( )
| A、3 | B、5 | C、6 | D、7 |
下列各式中,正确的是( )
A、
| |||
B、(-
| |||
C、±
| |||
D、
|
 如图,在Rt△ABC中,∠A=90°,∠C=30°,AB=8,若动点D从B出发沿线段BA以每秒2个单位长度运动到A点为止,过D作DE∥BC交于点E.设运动点D的运动时间为x秒,当x为何值时,△BDE的面积S有最大值?最大值为多少?
如图,在Rt△ABC中,∠A=90°,∠C=30°,AB=8,若动点D从B出发沿线段BA以每秒2个单位长度运动到A点为止,过D作DE∥BC交于点E.设运动点D的运动时间为x秒,当x为何值时,△BDE的面积S有最大值?最大值为多少?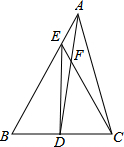 如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证:
如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证: 在矩形ABCD中,AB=3,BC=6,BE=2EC,DM⊥AE于点M,求DM.
在矩形ABCD中,AB=3,BC=6,BE=2EC,DM⊥AE于点M,求DM.