题目内容
3.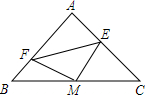 如图,在Rt△ABC中,AB=AC,∠A=90°,M为BC的中点,BF=AE,试判断△MEF是什么形状的三角形?并证明你的结论.
如图,在Rt△ABC中,AB=AC,∠A=90°,M为BC的中点,BF=AE,试判断△MEF是什么形状的三角形?并证明你的结论.
分析 由等腰直角三角形的性质得出AM=$\frac{1}{2}$BC=BM,AM平分∠BAC,AM⊥BC,∠B=∠C=45°,由SAS判定△BMF≌△AME,得出MF=ME,∠BMF=∠AME,再由角的互余关系得出∠EMF=90°,即可得出结论.
解答 解:△MEF是等腰直角三角形.理由如下: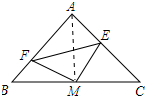
连接AM,如图所示:
∵M是BC的中点,∠BAC=90°,AB=AC
∴AM=$\frac{1}{2}$BC=BM,AM平分∠BAC,AM⊥BC,∠B=∠C=45°,
∴∠MAE=$\frac{1}{2}$∠BAC=45°,∠AMB=90°,
∴∠B=∠MAE,
在△BMF和△AME中,$\left\{\begin{array}{l}{BM=AM}&{\;}\\{∠B=∠MAE}&{\;}\\{BF=AE}&{\;}\end{array}\right.$,
∴△BMF≌△AME(SAS),
∴MF=ME,∠BMF=∠AME,
∵∠AMF+∠BMF=90°,
∴∠AMF+∠AME=90°,
即∠EMF=90°,
∴△MEF是等腰直角三角形.
点评 此题考查了等腰三角形的性质、等腰直角三角形的判定、全等三角形的判定与性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
18.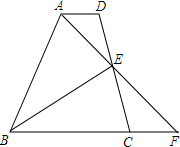 在梯形ABCD中,AD∥BC,E为CD的中点,BE⊥AE,AE的延长线交BC的延长线于点F.
在梯形ABCD中,AD∥BC,E为CD的中点,BE⊥AE,AE的延长线交BC的延长线于点F.
(1)求证:AE是∠BAD的平分线;
(2)当∠D=90°,∠ABC=60°,AB=12时,求AD的长.
 在梯形ABCD中,AD∥BC,E为CD的中点,BE⊥AE,AE的延长线交BC的延长线于点F.
在梯形ABCD中,AD∥BC,E为CD的中点,BE⊥AE,AE的延长线交BC的延长线于点F.(1)求证:AE是∠BAD的平分线;
(2)当∠D=90°,∠ABC=60°,AB=12时,求AD的长.
13.已知$\frac{3}{a}$=$\frac{4}{b}$,则$\frac{3a+2b}{a-b}$=( )
| A. | -17 | B. | -1 | C. | $\frac{17}{7}$ | D. | 17 |
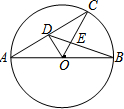 如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( )
如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( ) 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°. 已知:如图,O是AB的中点,DC∥AB.求证:AE=CF.
已知:如图,O是AB的中点,DC∥AB.求证:AE=CF.