题目内容
我们知道:sin30°=
,tan30°=
,sin45°=
,tan45°=1,sin60°=
,tan60°=
,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
考点:锐角三角函数的增减性,特殊角的三角函数值
专题:
分析:由直角三角形中斜边最长及锐角三角函数的定义可以证明:对于任意锐角α,都有tanα>sinα.
解答: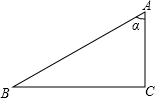 解:对于任意锐角α,都有tanα>sinα,理由如下:
解:对于任意锐角α,都有tanα>sinα,理由如下:
如图,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,设∠A=α.
则tanα=
,sinα=
,
∵b<c,
∴
>
,
∴tanα>sinα.
 解:对于任意锐角α,都有tanα>sinα,理由如下:
解:对于任意锐角α,都有tanα>sinα,理由如下:如图,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,设∠A=α.
则tanα=
| a |
| b |
| a |
| c |
∵b<c,
∴
| a |
| b |
| a |
| c |
∴tanα>sinα.
点评:本题考查了锐角三角函数的定义,在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.

练习册系列答案
相关题目
下列说法正确的是( )
| A、一个点可以确定一条直线 |
| B、平分弦的直径垂于直弦 |
| C、三个点可以确定一个圆 |
| D、在图形旋转中图形上可能存在不动点 |