题目内容
2. 如图,在矩形纸片ABCD中,AB=8,BC=6,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点F处,求AE长.
如图,在矩形纸片ABCD中,AB=8,BC=6,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点F处,求AE长.
分析 由勾股定理可求得BD=10,由翻折的性质可求得FB=8,EF=EA,EF⊥BD,设AE=EF=x,则BE=12-x,在Rt△BEF中,由勾股定理列方程求解即可.
解答  解:由折叠性质可知:DF=AD=BC=6,EF=EA,EF⊥BD.
解:由折叠性质可知:DF=AD=BC=6,EF=EA,EF⊥BD.
在Rt△BAD中,由勾股定理得:BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=10,
∵BF=BD-DF,
∴BF=10-6=4.
设AE=EF=x,则BE=8-x.
在Rt△BEF中,由勾股定理可知:EF2+BF2=BE2,即x2+16=(8-x)2,
解得:x=3.
∴AE=3.
点评 本题主要考查的是翻折的性质、勾股定理的应用,在Rt△BEF中,由勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
12.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. |  +4.5 | B. |  -1.5 | C. |  -0.4 | D. |  +0.6 |
 已知:∠AOB,点M、N.求作:
已知:∠AOB,点M、N.求作: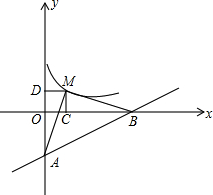 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.