Question

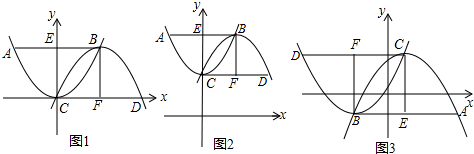
11．如图，已知?ABCD，点E在边AB上，连接CE并延长交DA的延长线于点F，若AE=AF，求证：AB=DF．

Answer 1

分析 由AE=AF，可得∠F=∠AEF，又由四边形ABCD是平行四边形，可证得∠AEF=∠DCF，CD=AB，继而证得△DCF是等腰三角形，继而证得：AB=DF．

解答 证明：∵AE=AF，
∴∠F=∠AEF，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴∠AEF=∠DCF，
∴∠F=∠DCF，
∴CD=DF，
∴AB=DF．

点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．注意证得△DCF是等腰三角形是关键．