题目内容
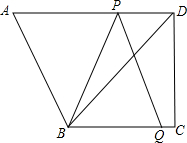 在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.(1)当t为何值时,AP=BQ;
(2)当t为何值时,△BPQ的面积和△BPD的面积相等;
(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三等形?
考点:四边形综合题
专题:
分析:(1)先用t表示AP和BQ,再建立等式即可求得;
(2)容易知△BPQ和△BPD高相等,只要使它们的底相等即可得△BPQ和△BPD的面积相等;
(3)以B,P,Q为顶点的三角形为等腰三角形有三种情况:当PB=PQ时,当PQ=BQ时,当BP=BQ时,由等腰三角形的性质就可以得出结论.
(2)容易知△BPQ和△BPD高相等,只要使它们的底相等即可得△BPQ和△BPD的面积相等;
(3)以B,P,Q为顶点的三角形为等腰三角形有三种情况:当PB=PQ时,当PQ=BQ时,当BP=BQ时,由等腰三角形的性质就可以得出结论.
解答:解:(1)∵PD=2t,∴AP=AD-PD=21-2t,
∵CQ=t,∴BQ=BC-CQ=16-t,
∵AP=BQ,
∴21-2t=16-t,
解得t=5;
(2)∵S△BPQ=S△BPD,△BPQ和△BPD高相等,
∴△BPQ和△BPD的底也相等,即PD=BQ,
则2t=16-t;
解得t=
;
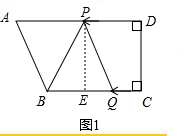
(3)如图1,当PB=PQ时,作PE⊥BC于E,
∴EQ=
BQ,
∵CQ=t,
∴BQ=16-t,
∴EQ=8-
t,
∴EC=8-
t+t=8+
t.
∴2t=8+
t.
解得:t=
.
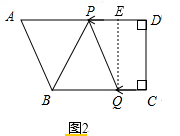
当PQ=BQ时,如图2,作QE⊥AD于E,
∴∠PEQ=∠DEQ=90°,
∵∠C=∠D=90°,
∴∠C=∠D=∠DEQ=90°,
∴四边形DEQC是矩形,
∴DE=QC=t,
∴PE=t,QE=CD=12.
在Rt△PEQ中,由勾股定理,得
PQ=
.
16-t=
,
解得:t=
;
当BP=PQ时,作PE⊥BC于E,
∴EQ=BE=
BQ,
∵CQ=t,
∴BQ=16-t,
∴BE=8-
t,
∴PB=
.
∴16-t=
.
解得:t1=16+8
,t2=16-8
∵0<t≤10.5
∴t=16-8
.
综上所述,t=
,
或16-8
时以B,P,Q三点为顶点的三角形为等腰三角形.
∵CQ=t,∴BQ=BC-CQ=16-t,
∵AP=BQ,
∴21-2t=16-t,
解得t=5;
(2)∵S△BPQ=S△BPD,△BPQ和△BPD高相等,
∴△BPQ和△BPD的底也相等,即PD=BQ,
则2t=16-t;
解得t=
| 16 |
| 3 |

(3)如图1,当PB=PQ时,作PE⊥BC于E,
∴EQ=
| 1 |
| 2 |
∵CQ=t,
∴BQ=16-t,
∴EQ=8-
| 1 |
| 2 |
∴EC=8-
| 1 |
| 2 |
| 1 |
| 2 |
∴2t=8+
| 1 |
| 2 |
解得:t=
| 16 |
| 3 |

当PQ=BQ时,如图2,作QE⊥AD于E,
∴∠PEQ=∠DEQ=90°,
∵∠C=∠D=90°,
∴∠C=∠D=∠DEQ=90°,
∴四边形DEQC是矩形,
∴DE=QC=t,
∴PE=t,QE=CD=12.
在Rt△PEQ中,由勾股定理,得
PQ=
| t2+144 |
16-t=
| t2+144 |
解得:t=
| 7 |
| 2 |
当BP=PQ时,作PE⊥BC于E,
∴EQ=BE=
| 1 |
| 2 |
∵CQ=t,
∴BQ=16-t,
∴BE=8-
| 1 |
| 2 |
∴PB=
-8t+
|
∴16-t=
-8t+
|
解得:t1=16+8
| 3 |
| 3 |
∵0<t≤10.5
∴t=16-8
| 3 |
综上所述,t=
| 16 |
| 3 |
| 7 |
| 2 |
| 3 |
点评:本题考查了勾股定理的运用,矩形的性质的运用,等腰三角形的性质的运用,一元二次方程的解法的运用,解答时根据等腰三角形的性质建立方程是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
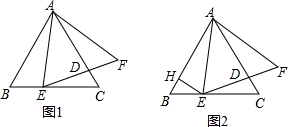
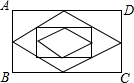 如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少?
如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少?