题目内容
3. 在平面直角坐标系xOy中,直线y=2x+2与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-$\frac{2}{3}$经过点A和点C(4,0).
在平面直角坐标系xOy中,直线y=2x+2与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-$\frac{2}{3}$经过点A和点C(4,0).(1)求该抛物线的表达式.
(2)连接CB,并延长CB至点D,使DB=CB,请判断点D是否在该抛物线上,并说明理由.
(3)在(2)的条件下,过点C作x轴的垂线EC与直线y=2x+2交于点E,以DE为直径画⊙M,
①求圆心M的坐标;
②若直线AP与⊙M相切,P为切点,直接写出点P的坐标.
分析 (1)根据题意可知 A(-1,0),B(0,2),待定系数法求出a和b的值,进而求出抛物线的解析式;
(2)过点D作DF垂直x轴于点F,利用三角形相似求出D点坐标,进而作出判断;
(3)①设DE与y轴的交点为M′,证明M′和M重合,进而求出M点的坐标;②分别设出圆的方程以及切线的方程,联立方程组求出k的值,进而求出点P的坐标.
解答 解:(1)依题意,可知 A(-1,0),B(0,2).
∵抛物线y=ax2+bx-$\frac{2}{3}$经过点A,C (4,0),
∴$\left\{\begin{array}{l}{a-b-\frac{2}{3}=0}\\{16a+4b-\frac{2}{3}=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=\frac{1}{6}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴y=$\frac{1}{6}$x2-$\frac{1}{2}$x-$\frac{2}{3}$;
(2)点D在该抛物线上.
依题意,可得BO=2,CO=4.
过点D作DF垂直x轴于点F,如图1,
∴△CDF∽△CBO.
∴$\frac{DC}{BC}=\frac{DF}{BO}=\frac{CF}{CO}=\frac{2}{1}$.
∴DF=4,OF=CF-OC=4.
∴D(-4,4).
∵$\frac{1}{6}$×(-4)2-$\frac{1}{2}$×(-4)-$\frac{2}{3}$=4,
∴点D在该抛物线上.
(3)①由题意可知E(4,10).
设DE与y轴的交点为M′,
∵M′B∥EC,
∴$\frac{DM′}{EM′}=\frac{DB}{CB}=1$.
∴D M′=EM′.
∴M′即⊙M的圆心M.
∴BM=$\frac{1}{2}$EC=5.
∴M(0,7).
②如图2,设圆的方程为x2+(y-7)2=25,切线方程为ky=x+1,
联立两方程得到:(ky-1)2+(y-7)2=25,
即(k2+1)y2-(2k+14)y+25=0,
△=12k2-7k-12=0,
解得k=$\frac{4}{3}$或k=-$\frac{3}{4}$,
当k=-$\frac{3}{4}$时,解得y=4,
当x=4时,x=-4,
即切点坐标为(-4,4);
当k=$\frac{4}{3}$时,联立方程组解得y=3,
当y=3时,x=3,
此时的切点坐标为(3,3);
综上:点P的坐标是(-4,4)或(3,3).
点评 本题考查了二次函数综合题的知识,此题涉及到待定系数法求二次函数解析式,相似三角形的判定与性质、圆的知识,解答(2)问关键是求出点D的坐标,解答(3)问关键是正确地画出图形.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案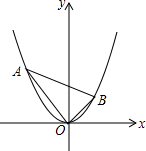 如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )
如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | ac2<bc2 | B. | c-a<c-b | C. | a-c<b-c | D. | $\frac{a}{c}<\frac{b}{c}$ |
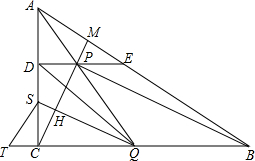 如图,Rt△ABC中,∠C=90°,D点和E点在AC,AB边上,且DE∥BC.P为线段DE上一点,使得∠CPB=90°,CP的延长线交AB于点M,延长AP交BC于点Q,过Q作PB的平行线交PC于点H,交AC于点S,T为BC延长线上一点,且满足$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$,连接TS.求证:TS⊥DQ.
如图,Rt△ABC中,∠C=90°,D点和E点在AC,AB边上,且DE∥BC.P为线段DE上一点,使得∠CPB=90°,CP的延长线交AB于点M,延长AP交BC于点Q,过Q作PB的平行线交PC于点H,交AC于点S,T为BC延长线上一点,且满足$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$,连接TS.求证:TS⊥DQ.