题目内容
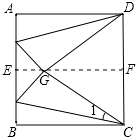 如图,先将正方形ABCD对折,折痕为EF,把这个正方形展平后,再将AD边沿经过D点的一直线折叠,BC边沿经过C点的一直线折叠,使点A、点B都与折痕EF上的点G重合,则∠1等于
如图,先将正方形ABCD对折,折痕为EF,把这个正方形展平后,再将AD边沿经过D点的一直线折叠,BC边沿经过C点的一直线折叠,使点A、点B都与折痕EF上的点G重合,则∠1等于分析:因为CF为
倍的BC,点G为A折叠后对应的点,所以AD=DG,在直角三角形GDF中,GD=2DF,所以∠DGF=30°,又G为B对折后对应的点,所以∠BCG=2∠1=∠CGF,由此可求的∠1的度数.
| 1 |
| 2 |
解答:解:∵正方形ABCD,
∴AB=BC=CD=AD
由折叠可知:AD=DG,BC=CG,
∴DG=CG=CD,
∴△DCG为等边三角形,
由折叠可知:F为CD中点,
∴FC=
CD=
CG,∠GFC=90°,
在直角三角形GCF中,2CF=CG,∴∠CGF=30°,
∵∠EFC+∠BCD=180°,
∴EF∥BC,
∴∠GCB=∠CGF=30°,
由折叠可知:∠1=
∠GCB=15°.

∴AB=BC=CD=AD
由折叠可知:AD=DG,BC=CG,
∴DG=CG=CD,
∴△DCG为等边三角形,
由折叠可知:F为CD中点,
∴FC=
| 1 |
| 2 |
| 1 |
| 2 |
在直角三角形GCF中,2CF=CG,∴∠CGF=30°,
∵∠EFC+∠BCD=180°,
∴EF∥BC,
∴∠GCB=∠CGF=30°,
由折叠可知:∠1=
| 1 |
| 2 |
点评:本题考查的是图形对折的性质,对折后形成的图形与其对应的图形全等,即对应的边、角对应相等.

练习册系列答案
相关题目
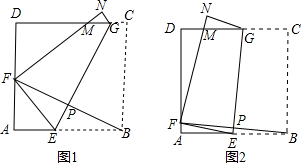 下一个正确结论(或结果):
下一个正确结论(或结果):
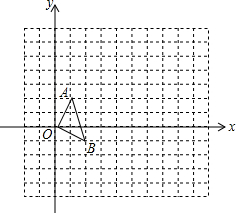 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).


 如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=________.
如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=________.