Question

（2010•房山区一模）阅读下列材料：
小明遇到一个问题：如图1，正方形ABCD中，E、F、G、H分别是AB、BC、CD和DA边上靠近A、B、C、D的n等分点，连接AF、BG、CH、DE，形成四边形MNPQ．求四边形MNPQ与正方形ABCD的面积比（用含n的代数式表示）．
小明的做法是：
先取n=2，如图2，将△ABN绕点B顺时针旋转90゜至△CBN′，再将△ADM绕点D逆时针旋转90゜至△CDM′，得到5个小正方形，所以四边形MNPQ与正方形ABCD的面积比是

1

5

；
然后取n=3，如图3，将△ABN绕点B顺时针旋转90゜至△CBN′，再将△ADM绕点D逆时针旋转90゜至△CDM′，得到10个小正方形，所以四边形MNPQ与正方形ABCD的面积比是

4

10

，即

2

5

；
请你参考小明的做法，解决下列问题：
（1）在图4中探究n=4时四边形MNPQ与正方形ABCD的面积比（在图4上画图并直接写出结果）；
（2）图5是矩形纸片剪去一个小矩形后的示意图，请你将它剪成三块后再拼成正方形（在图5中画出并指明拼接后的正方形）．

Answer 1

分析：（1）根据四等分点再找出其它的等分点，仿照图3的作法画出图形，然后再查出旋转后的正方形的个数是17，中间四边形中正方形的个数是9，然后计算即可求解；
（2）根据面积是10，所以拼接后的正方形的边长是

10

，然后根据网格的特点进行剪接．

解答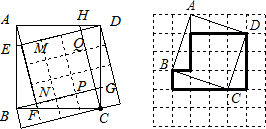：  解（1）如图1，
正方形ABCD的面积是17个小正方形，四边形MNPQ是9个小正方形，
∴四边形MNPQ与正方形ABCD的面积比为：

9

17

；        
 （2）如图2，
设每个小正方形的面积是1，图形面积是10，
所以拼接后的正方形的边长是

10

，
拼接后的正方形是正方形ABCD．

点评：本题考查了图形的剪拼；用到的知识点是正方形的性质，旋转的性质，以及设计作图，难度不大，读懂题目提供的信息是解题的关键．