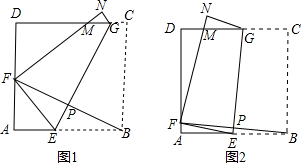
如图.先将正方形ABCD沿EF对折使AB与DC完全重合.再将角D翻折.使点D落在EF上.折痕为CG.那么∠DCG= ．题目和参考答案——青夏教育精英家教网—

如图，先将正方形ABCD沿EF对折使AB与DC完全重合，再将角D翻折，使点D落在EF上，折痕为CG，那么∠DCG=________．

15°
分析：根据折叠的性质可得CF= $\text{[math]}$ BC= $\text{[math]}$ DC，DC=CD'，从而可求出∠CD'F=30°，∠DCD'=30°，也可得出∠DCG的度数．
解答：由折叠的性质得，CF= $\text{[math]}$ BC= $\text{[math]}$ DC，DC=CD'，
故在直角三角形CD'F中可得出，∠CD'F=30°，
∵DC∥EF，
∴∠DCD'=30°，
由折叠的性质得，∠DCG=∠D'CG= $\text{[math]}$ ∠DCD'=15°．
故答案为：15°．
点评：此题考查了折叠的性质及含30°角的直角三角形的性质，解答本题的关键是掌握翻折前后对应线段相等，对应角相等，难度一般．

练习册系列答案

相关题目

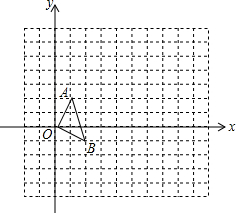【问题】在正方形网格中，如图（一），△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．
（1）以点O（0，0）为位似中心，按比例尺3：1在位似中心的同侧将△OAB放大为△OA′B′，放大后点A、B的对应点分别为A′、B′．画出△OA′B′，并写出点A'、B'的坐标：A′（

，

），B′（

，

-3

）；
（2）在（1）中，若点C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标（

，

）；
【拓展】在平面内，先将一个多边形以点O为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为k，并且原多边形上的任一点P，它的对应点P'在线段OP或其延长线上；接着将所得多边形以点O为旋转中心，逆时针旋转一个角度θ，这种经过和旋转的图形变换叫做旋转相似变换，记为O（k，θ），其中点O叫做旋转相似中心，k叫做相似比，θ叫做旋转角．
【探索】如图（二），完成下列问题：
（3）填空：如图1，将△ABC以点A为旋转相似中心，放大为原来的2倍，再逆时针旋转60°，得到△ADE，这个旋转相似变换记为A（

，

60°

）；
（4）如图2，△ABC是边长为3cm的等边三角形，将它作旋转相似变换A(

，90°)，得到△ADE，求线段BD的长．

如图，先将正方形ABCD沿EF对折使AB与DC完全重合，再将角D翻折，使点D落在EF上，折痕为CG，那么∠DCG=________．

试题分类