题目内容
7.若3x2-2x+b和x2+bx-3的差中不存在含x的项,试求b的值,写出它们的差,并说明不论x取什么值,它们的差总是正数.分析 先求出3x2-2x+b和x2+bx-3的差,然后根据不存在含x的项求出b的值,最后进行判断证明.
解答 解:(3x2-2x+b)-(x2+bx-3)
=3x2-2x+b-x2-bx+3
=2x2-(b+2)x+b+3,
∵差中不含x项,
∴b+2=0,
解得:b=-2,
当b=-2时,
差=2x2+1,
∵不论x取何值,x2为非负数,
故2x2+1为正数.
点评 本题考查了整式的加减,解答本题的关键是掌握去括号、合并同类项的法则.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
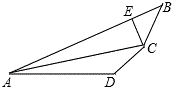 如图,AC平分∠BAD,CE⊥AB,且2AE=AB+AD,试探索∠ADC与∠ABC的关系.
如图,AC平分∠BAD,CE⊥AB,且2AE=AB+AD,试探索∠ADC与∠ABC的关系.