Question

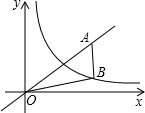如图，B为双曲线y=

k

x

（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，若OB²-AB²=12，则k=

6

．

Answer 1

分析：延长AB交x轴于点C，设点C的横坐标为a，再根据AB∥y轴表示出BC与AB的长度，在Rt△BOC中，利用勾股定理表示出OB²，再代入已知条件整理即可消掉a并求出k值．

解答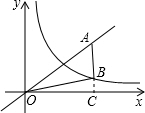：解：如图，延长AB交x轴于点C，设点C的横坐标为a，
则点B的纵坐标为

k

a

，点A的纵坐标为a，
所以，AB=a-

k

a

，
∵AB平行于y轴，
∴AC⊥OC，
在Rt△BOC中，OB²=OC²+BC²=a²+（

k

a

）²，
∵OB²-AB²=12，
∴a²+（

k

a

）²-（a-

k

a

）²=12，
整理得，2k=12，
解得k=6．
故答案为：6．

点评：本题考查了待定系数法求反比例函数解析，一次函数图象上点的坐标特征，勾股定理的应用，利用点C的横坐标表示出点A、B的纵坐标是解题的关键．