Question

如图，C为双曲线y=

k

x

（x＞0）上一点，线段AE与y轴交于点E，且AE=EC，将线段AC平移至BD处，点D恰好也在双曲线y=

k

x

（x＞0）上，若A（-1，0），B（0，-2）．则k=

4

．

Answer 1

分析：首先根据已知得出△NCE≌△OAE，进而得出C点横坐标，进而利用平移的性质得出C，D两点坐标，即可得出k的值．

解答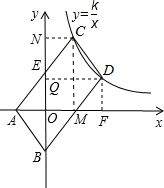：解：过点C作CN⊥y轴于点N，CM⊥x轴于点M，DQ⊥y轴于点Q，DF⊥x轴于点F，
在△NCE与△OAE中，
∵

EC=AE ∠CNE=∠AOE ∠NEC=∠OEA

，
∴△NCE≌△OAE，
∴AO=NC=1，
则设C点坐标为：（1，y），
∵A（-1，0），B（0，-2），又因为线段AC平移至BD处，
∴D点坐标为：（2，y-2），
∵C，D都在反比例函数图象上，
∴1×y=k，2（y-2）=k，
∴y=2（y-2），
解得：y=4，
∴C点坐标为：（1，4），
∴k=1×4=4．
故答案为：4．

点评：此题主要考查了平移的性质以及反比函数的性质，根据已知得出C，D两点坐标是解题关键．