题目内容
6．
如图，OC⊥AB于点O，OD平分∠BOC，求∠AOD的度数．
分析 先由垂直的定义得出∠BOC=90°，再根据角平分线定义求出∠BOD=$\frac{1}{2}$∠BOC=45°，然后利用邻补角定义得出∠AOD=180°-∠BOD计算即可求解．
解答 解：∵OC⊥AB于点O，
∴∠BOC=90°，
∵OD平分∠BOC，
∴∠BOD=$\frac{1}{2}$∠BOC=45°，
∴∠AOD=180°-∠BOD=135°．
点评 本题考查了垂直的定义，角平分线定义和邻补角互补的性质，要注意领会由垂直得直角这一要点．
练习册系列答案
相关题目
5．
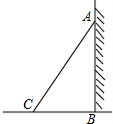如图，一架长为10m的梯子AB斜靠在墙上，梯子的顶端距地面的垂直距离为8m．
（1）求梯子底端C到墙的底边的垂直距离BC；
（2）如果梯子的顶端下滑1m，那么它的底端是否也滑动1m（精确到0.1m）？
如图，一架长为10m的梯子AB斜靠在墙上，梯子的顶端距地面的垂直距离为8m．（1）求梯子底端C到墙的底边的垂直距离BC；
（2）如果梯子的顶端下滑1m，那么它的底端是否也滑动1m（精确到0.1m）？
14．苹果熟了，小明帮助妈妈到集贸市场去卖刚刚采摘下来的苹果．已知销售数量x与售价y的关系如下：
（1）上表反映了哪两个量之间的关系？
（2）根据表格中的数据，售价y是怎样随销售量的变化而变化的？
（3）小明的妈妈让小明买10kg的苹果，并给了他25元．问给的钱够吗？若不够，差多少钱？若富余，剩多少钱？
| 数量x（千克） | 1 | 2 | 3 | 4 | 5 |
| 售价y（元） | 2.1 | 4.2 | 6.3 | 8.4 | 10.5 |
（2）根据表格中的数据，售价y是怎样随销售量的变化而变化的？
（3）小明的妈妈让小明买10kg的苹果，并给了他25元．问给的钱够吗？若不够，差多少钱？若富余，剩多少钱？
如图所示，O为直线AE上一点，OC平分∠BOD，∠1与∠2互余，∠2=44°，试比较∠AOC与∠COE的大小．