题目内容
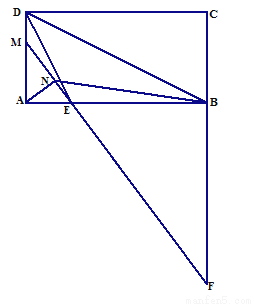
如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+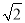 BN.
BN.
练习册系列答案
相关题目
题目内容
如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+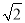 BN.
BN.
