题目内容
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
(1)如图①,![]() 中,
中,![]() ,若
,若![]() ,点
,点![]() 是斜边
是斜边![]() 上一动点,求线段
上一动点,求线段![]() 的最小值.
的最小值.

在组内经过合作交流,得到了如下的解决方法:
根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:
当![]() 时,线段
时,线段![]() 取得最小值.请你根据小明的思路求出这个最小值.
取得最小值.请你根据小明的思路求出这个最小值.
(思维运用)
(2)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一动点,过
上一动点,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求线段
,求线段![]() 的最小值.
的最小值.

(问题拓展)
(3)如图,![]() ,
,![]() 线段
线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() 在一条直线上.
在一条直线上.![]() ,
,![]() 分别是对角线
分别是对角线![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 之间的距离的最小值为_____.(直接写出结果,不需要写过程)
之间的距离的最小值为_____.(直接写出结果,不需要写过程)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的面积相等即可求解;
(2)连接CM,先证明四边形CDME是矩形,得出DE=CM,再由三角形的面积关系求出CM的最小值,即可得出结果.
(3)连接PM、PN.首先证明∠MPN=90°,设PA=2a,则PB=6-2a,PM=a,PN=![]() (3-a),构建二次函数,利用二次函数的性质即可解决问题;
(3-a),构建二次函数,利用二次函数的性质即可解决问题;
解:(1)如图,当![]() 时,线段
时,线段![]() 取得最小值.
取得最小值.
∵![]() 中,
中,![]() ,
,![]() ,
,
∴AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故CM的最小值为![]() .
.
(2)连接CM,如图所示:
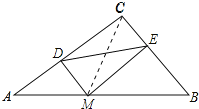
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB=![]()
当CM⊥AB时,CM最短,
∵![]()
∴![]() ,
,
∴![]()
∴线段DE的最小值为![]() ;
;
故答案为:![]() .
.
(3)连接PM、PN.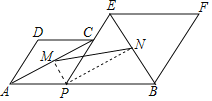
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠CPM=![]() ∠APC=60°,∠EPN=
∠APC=60°,∠EPN=![]() ∠EPB=30°,
∠EPB=30°,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=6-2a,PM=a,PN=![]() (3-a),
(3-a),
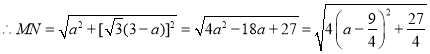 ,
,
∴a=![]() 时,点M,N之间的距离最短,最短距离为
时,点M,N之间的距离最短,最短距离为![]() ,
,
故答案为:![]() .
.