题目内容
如图，M是CD的中点，EM⊥CD，若CD=4cm，EM=6cm，则弧CED所在圆的半径为 cm．
【答案】分析：根据EM⊥CD，则CM=
CD=2cm，连接OC，在直角三角形OCM中，根据勾股定理就得到方程求解即可．
解答：
解：EM⊥CD
则CM=
CD=2cm
连接OC，在直角三角形OCM中，若设半径是r，则OC=r，OM=6-r
根据勾股定理就得到方程：r2=4+（6-r）2
解得：r=
．
弧CED所在圆的半径为
cm．
点评：本题考查了垂径定理，利用勾股定理转化为解方程的问题．
CD=2cm，连接OC，在直角三角形OCM中，根据勾股定理就得到方程求解即可．解答：
解：EM⊥CD则CM=
CD=2cm连接OC，在直角三角形OCM中，若设半径是r，则OC=r，OM=6-r
根据勾股定理就得到方程：r2=4+（6-r）2
解得：r=
．弧CED所在圆的半径为
cm．点评：本题考查了垂径定理，利用勾股定理转化为解方程的问题．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
如图，M是CD的中点，EM⊥CD，CD=2cm，EM=5cm，则
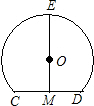如图，M是CD的中点，EM⊥CD，若CD=4cm，EM=6cm，则弧CED所在圆的半径为
（2013•黄冈）如图，M是CD的中点，EM⊥CD，若CD=4，EM=8，则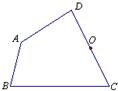
18、如图，O是CD的中点．以O为位似中心，用直尺和圆规作四边形ABCD的一个位似图形，使四边形ABCD的边长放大到原来的2倍．（保留作图痕迹，不必写出作法）