题目内容
10.已知a、b、c是△ABC的三边长,若|a-b|+|a2+b2-c2|=0,则△ABC是等腰直角三角形.分析 首先根据题意由非负数的性质可得:a-b=0,a2+b2-c2=0,进而得到a=b,a2+b2=c2,根据勾股定理逆定理可得△ABC的形状为等腰直角三角形.
解答 解:∵|a-b|+|a2+b2-c2|=0,
∴a-b=0,a2+b2-c2=0,
解得:a=b,a2+b2=c2,
∴△ABC是等腰直角三角形.
故答案为:等腰直角三角形.
点评 此题主要考查了勾股定理逆定理以及非负数的性质,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.关于函数y=$\frac{-{k}^{2}-2}{x}$,下列说法中错误的是( )
| A. | 当x>0时,y随x的增大而增大 | |
| B. | 当x<0时,y随x的增大而增大 | |
| C. | 当x=1时的函数值大于x=-1时的函数值 | |
| D. | 在函数图象所在的每个象限内,y都随x的增大而增大 |
1. 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
19.在同一平面直角坐标系内,将函数y=x2+4x+1的图象沿x轴向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
| A. | (-1,1) | B. | (0,-4) | C. | (2,-2) | D. | (1,-1) |

 将如图所示的平面展开图折叠成正方体,则a对面的数字是-1.
将如图所示的平面展开图折叠成正方体,则a对面的数字是-1. 如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.
如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.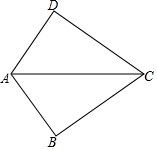 如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.
如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.