题目内容
 如图,在6×11的正方形网格中有一只可爱的小狐狸,算算看画面中由实线组成的相似三角形有( )
如图,在6×11的正方形网格中有一只可爱的小狐狸,算算看画面中由实线组成的相似三角形有( )| A、4对 | B、3对 | C、2对 | D、1对 |
分析:本题主要应用两三角形相似的判定定理,三组对应边的比相等,做题即可.
解答: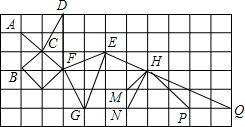 解:设第一个小正方形的边长为1,则计算各个小三角形的各边长
解:设第一个小正方形的边长为1,则计算各个小三角形的各边长
△ABC的各边分别为2、
、
;
△CDF的各边分别为
、
、3;
△EFG的各边分别为
、
、
;
△HMN的各边分别为1、
、
;
△HPQ的各边分别为2、2
、2
.
可以得出△ABC与△EFG,△HMN与△HPQ的各边对应成比例且比例相等,所以这两组三角形相似.
故选C.
 解:设第一个小正方形的边长为1,则计算各个小三角形的各边长
解:设第一个小正方形的边长为1,则计算各个小三角形的各边长△ABC的各边分别为2、
| 2 |
| 2 |
△CDF的各边分别为
| 2 |
| 5 |
△EFG的各边分别为
| 5 |
| 5 |
| 10 |
△HMN的各边分别为1、
| 2 |
| 5 |
△HPQ的各边分别为2、2
| 2 |
| 5 |
可以得出△ABC与△EFG,△HMN与△HPQ的各边对应成比例且比例相等,所以这两组三角形相似.
故选C.
点评:此题主要考查学生对三组对应边的比相等的三角形相似的运用.

练习册系列答案
相关题目
 30、如图,一首轮船向正东方向航行,上午9时测得它在灯塔P的南偏西26°方向,距离灯塔120海里的点M处,上午11时到达这座灯塔的正南方向的点N处,那么这艘轮船在这段时间内航行的平均速度是多少?(精确到0.01海里)
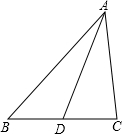
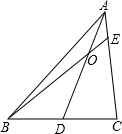
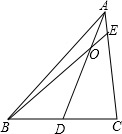
30、如图,一首轮船向正东方向航行,上午9时测得它在灯塔P的南偏西26°方向,距离灯塔120海里的点M处,上午11时到达这座灯塔的正南方向的点N处,那么这艘轮船在这段时间内航行的平均速度是多少?(精确到0.01海里) 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
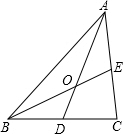
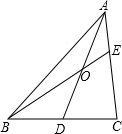
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=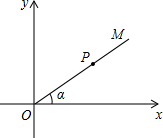 (2011•长宁区一模)如图,在直角坐标系中,∠α的顶点与坐标原点O重合,一边在x轴正半轴上,另一边是射线OM.已知cotα=
(2011•长宁区一模)如图,在直角坐标系中,∠α的顶点与坐标原点O重合,一边在x轴正半轴上,另一边是射线OM.已知cotα=