题目内容
2. 如图所示,在直角△ABC中,∠C=90°,AC=4,BC=3,MN⊥AB,且S△AMN=$\frac{1}{4}$S△ABC,则四边形BCMN的外接圆的半径等于$\frac{3\sqrt{5}}{4}$.
如图所示,在直角△ABC中,∠C=90°,AC=4,BC=3,MN⊥AB,且S△AMN=$\frac{1}{4}$S△ABC,则四边形BCMN的外接圆的半径等于$\frac{3\sqrt{5}}{4}$.
分析 连接BM根据相似三角形的性质得到$\frac{AN}{AC}=\frac{MN}{BC}=\frac{1}{2}$,求得AN=2,MN=$\frac{3}{2}$,根据勾股定理得到BM=$\sqrt{B{N}^{2}+M{N}^{2}}$=$\frac{3\sqrt{5}}{2}$,推出BM是⊙O的直径,于是得到结论.
解答 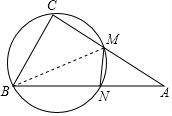 解:连接BM,∵∠BAC=∠MAN,∠ACB=∠ANM=90°,
解:连接BM,∵∠BAC=∠MAN,∠ACB=∠ANM=90°,
∴△ABC∽△AMN,
∵S△AMN=$\frac{1}{4}$S△ABC,
∴$\frac{AN}{AC}=\frac{MN}{BC}=\frac{1}{2}$,
∴AN=2,MN=$\frac{3}{2}$,
∵AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∴BN=AB-AN=3,
∴BM=$\sqrt{B{N}^{2}+M{N}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵∠C=90°,
∴BM是⊙O的直径,即四边形BCMN的外接圆的直径,
∴四边形BCMN的外接圆的半径=$\frac{1}{2}$BM=$\frac{3\sqrt{5}}{4}$.
故答案为:$\frac{3\sqrt{5}}{4}$.
点评 本题考查了三角形的外接圆与外心,勾股定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,DE∥BC、AD=3,BD=4,BF=3.5,EG=1.2,则DG=1.5,FC=2.8,若AF平分∠BAC,则EC=3.2.
如图,DE∥BC、AD=3,BD=4,BF=3.5,EG=1.2,则DG=1.5,FC=2.8,若AF平分∠BAC,则EC=3.2.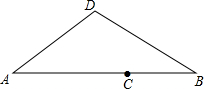 如图,点C是线段AB的黄金分割点(AC>BC),如果分别以点A、B为圆心,以AC的长为半径作弧相交于点D,那么∠DAB的度数是36°.
如图,点C是线段AB的黄金分割点(AC>BC),如果分别以点A、B为圆心,以AC的长为半径作弧相交于点D,那么∠DAB的度数是36°.