Question

11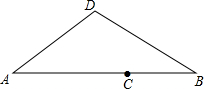．如图，点C是线段AB的黄金分割点（AC＞BC），如果分别以点A、B为圆心，以AC的长为半径作弧相交于点D，那么∠DAB的度数是36°．

Answer 1

分析 根据黄金分割的定义得到AC²=BC•AB，而AC=AD=BD，则BD²=BC•AB，根据相似三角形的判定得△BDC∽△BAD，则∠A=∠BDC，设∠A=x，则∠B=x，∠BDC=x，根据三角形外角性质得∠ACD=∠BDC+∠B=2x，所以∠ADC=∠ACD=2x，然后根据三角形内角和定理得到x+2x+x+x=180°，再解方程即可．

解答 解：连接DC，
∵点C是线段AB的一个黄金分割点，
∴AC²=BC•AB，
∵AD=AC=BD，
∴BD²=BC•AB，
即BD：BC=AB：BD，
而∠ABD=∠DBC，
∴△BDC∽△BAD，
∴∠A=∠BDC，
设∠A=x，则∠B=x，∠BDC=x，
∴∠ACD=∠BDC+∠B=2x，
而AC=AD，
∴∠ADC=∠ACD=2x，
∴x+2x+x+x=180°，解得x=36°，
即∠A=36°．
故答案为：36°．

点评 本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．