Question

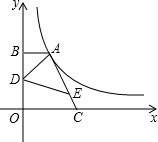如图，点A在双曲线y=

k

x

的第一象限的那一支上，AB⊥y轴于点B，点C在x轴正半轴上，且OC=2AB，点E在线段AC上，且AE=3EC，点D为OB的中点，若△ADE的面积为

3

2

，则k的值为

 

．

Answer 1

考点：反比例函数综合题

专题：探究型

分析：连接CD，由AE=3EC，△ADE的面积为

3

2

，得到△CDE的面积为

1

2

，则△ADC的面积为2，设A点坐标为（a，b），则k=ab，AB=a，OC=2AB=2a，BD=OD=

1

2

b，利用S_梯形OBAC=S_△ABD+S_△ADC+S_△ODC即可得出ab的值进而得出结论．

解答：解：连CD，如图，
∵AE=3EC，△ADE的面积为

3

2

，
∴△CDE的面积为

1

2

，
∴△ADC的面积为2，
设A点坐标为（a，b），则AB=a，OC=2AB=2a，
∵点D为OB的中点，
∴BD=OD=

1

2

b，
∵S_梯形OBAC=S_△ABD+S_△ADC+S_△ODC，
∴

1

2

（a+2a）×b=

1

2

a×

1

2

b+2+

1

2

×2a×

1

2

b，
∴ab=

8

3

，
把A（a，b）代入双曲线y=

k

x

得，
∴k=ab=

8

3

．
故答案为：

8

3

．

点评：本题考查了反比例函数综合题，熟知若点在反比例函数图象上，则点的横纵坐标满足其解析式；利用三角形的面积公式和梯形的面积公式建立等量关系等知识是解答此题的关键．