题目内容
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
则当x=1时,y的值为 .
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -17 | -3 | 7 | 13 | 15 | 13 |
考点:二次函数的性质
专题:
分析:当y=13时,x=-4或-2,根据抛物线的对称性可知,抛物线的对称轴为x=
=-3,故x=1和x=-7时,对应的函数值相等.
| -4-2 |
| 2 |
解答:解:根据抛物线的对称性,观察表格可知,
抛物线的对称轴为x=-3,
所以x=1和x=-7时,y=-17.
故本题答案为-17.
抛物线的对称轴为x=-3,
所以x=1和x=-7时,y=-17.
故本题答案为-17.
点评:本题考查了二次函数的对称性,观察表格,确定抛物线的对称轴是解题的关键.

练习册系列答案
相关题目
函数y=-
的图象经过的点是( )
| 2 |
| x |
| A、(-1,2) | ||
| B、(-1,-2) | ||
| C、(2,1) | ||
D、(-
|
不等式组
的解集是( )
|
| A、x≥1 |
| B、x>-3 |
| C、-3<x≤1 |
| D、x>-3或x≤1 |
 如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题: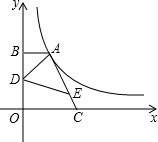 如图,点A在双曲线y=
如图,点A在双曲线y=