题目内容
8.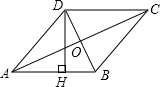 如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于$\frac{48}{5}$.
如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于$\frac{48}{5}$.
分析 先根据菱形的性质得OA=OC,OB=OD,AC⊥BD,再利用勾股定理计算出AB=10,然后根据菱形的面积公式得到$\frac{1}{2}$•AC•BD=DH•AB,再解关于DH的方程即可.
解答 解:∵四边形ABCD是菱形,
∴OA=OC=8,OB=OD=6,AC⊥BD,
在Rt△AOB中,AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=10,
∵S菱形ABCD=$\frac{1}{2}$•AC•BD,
S菱形ABCD=DH•AB,
∴DH•10=$\frac{1}{2}$×12×16,
∴DH=$\frac{48}{5}$.
故答案为:$\frac{48}{5}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如果正n边形的一个外角是40°,则n的值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
13.某公司前年缴税40万元,今年缴税48.4万元,设该公司这两年缴税的年均增长率为x,则根据题意所列的方程为( )
| A. | 40(1+x)2=48.4 | B. | 48.4(1+x)2=40 | C. | 40(1+2x)=48.4 | D. | 40(1-x)2=48.4 |
18.$\sqrt{(-4)^{2}}$的算术平方根是( )
| A. | ±2 | B. | ±4 | C. | 2 | D. | 4 |
 如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,
如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,