题目内容
17. 如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,
如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,(1)求CF:BF;
(2)AE与EF有何位置关系?证明你的结论.
分析 (1)直接根据相似三角形的性质即可得出结论;
(2)根据直角三角形的性质即可得出结论.
解答 即:(1)∵点E是CD的中点,
∴DE=CE.
∵△ADE∽△ECF,
∴$\frac{CF}{EF}$=$\frac{DE}{AD}$=$\frac{1}{2}$;
(2)AE⊥EF.
理由:∵△ADE∽△ECF,
∴∠CEF=∠DAE.
∵∠AED+∠DAE=90°,
∴∠AED+∠CEF=90°,即AE⊥EF.
点评 本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
5.下列方程中,解为x=-2的方程是( )
| A. | 3x-2=2x | B. | 4x-1=2x-3 | C. | 3x+1=2x-1 | D. | 5x-3=6x-2 |
7.小明在做电学实验时,记录下电压y(v)与电流x(A)有如下表所示的对应关系
(1)求y与x之间的函数解析式;(不要求写自变量的取值范围)
(2)当电流是5A时,电压是多少?
| x(A) | … | 2 | 4 | 6 | 8 | … |
| y(v) | … | 15 | 12 | 9 | 6 | … |
(2)当电流是5A时,电压是多少?
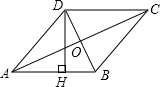 如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于$\frac{48}{5}$.
如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于$\frac{48}{5}$. 如图,在△ABC中,AB=4,BC=3,将BC沿BE方向折过去,使点C落在BA上的D点,折痕为BE,则AD的长为1.
如图,在△ABC中,AB=4,BC=3,将BC沿BE方向折过去,使点C落在BA上的D点,折痕为BE,则AD的长为1. a,b,c三个数在数轴上的位置如图所示,且|a|=|c|,化简:|a|-|b+a|+|b-c|-c+|c+a|.
a,b,c三个数在数轴上的位置如图所示,且|a|=|c|,化简:|a|-|b+a|+|b-c|-c+|c+a|. 已知有理数a,b,c在数轴上的位置如图所示,化简|a-b|-|c-a|=b+c-2a.
已知有理数a,b,c在数轴上的位置如图所示,化简|a-b|-|c-a|=b+c-2a.