题目内容
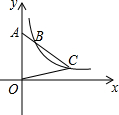 如图,点B、C在反比例函数y=
如图,点B、C在反比例函数y=| k |
| x |
| 1 |
| 2 |
考点:反比例函数系数k的几何意义,相似三角形的判定与性质
专题:
分析:过点B作BD⊥y轴于点D,过点C作CE⊥y轴于点E,连接OB,根据反比例函数系数k的几何意义可得S△ODB=S△OEC=
,易证△ABD∽△ACE,然后结合条件AB=
BC可求得AB=
AC,BC=
AC,S△OBC=
S△OAC=4,设DB=a,则OD=
,EC=3a,OE=
,然后运用割补法可推出S△OBC=S梯形DBCE,由此即可求出k的值.
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| k |
| a |
| k |
| 3a |
解答: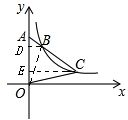 解:过点B作BD⊥y轴于点D,过点C作CE⊥y轴于点E,连接OB,如图,
解:过点B作BD⊥y轴于点D,过点C作CE⊥y轴于点E,连接OB,如图,
则有S△ODB=S△OEC=
,DB∥EC,
∴△ABD∽△ACE,
∴
=
=
.
∵AB=
BC,
∴AB=
AC,BC=
AC,
∴DB=
EC,S△OBC=
S△OAC=
×6=4.
设DB=a,则OD=
,EC=3a,OE=
,
∴S△OBC=S四边形ODBC-S△ODB
=S梯形DBCE+S△OEC-S△ODB
=S梯形DBCE=
(a+3a)(
-
)
=
=4,
∴k=3.
故答案为3.
 解:过点B作BD⊥y轴于点D,过点C作CE⊥y轴于点E,连接OB,如图,
解:过点B作BD⊥y轴于点D,过点C作CE⊥y轴于点E,连接OB,如图,则有S△ODB=S△OEC=
| 1 |
| 2 |
|
∴△ABD∽△ACE,
∴
| DB |
| EC |
| AB |
| AC |
| 1 |
| 3 |
∵AB=
| 1 |
| 2 |
∴AB=
| 1 |
| 3 |
| 2 |
| 3 |
∴DB=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
设DB=a,则OD=
| k |
| a |
| k |
| 3a |
∴S△OBC=S四边形ODBC-S△ODB
=S梯形DBCE+S△OEC-S△ODB
=S梯形DBCE=
| 1 |
| 2 |
| k |
| a |
| k |
| 3a |
=
| 4k |
| 3 |
∴k=3.
故答案为3.
点评:本题主要考查了反比例函数系数k的几何意义、相似三角形的判定与性质等知识,在解决问题的过程中用到了割补法、面积法等重要的数学方法,运用割补法推出S△OBC=S梯形DBCE是解决本题的关键.

练习册系列答案
相关题目
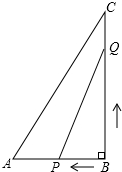 如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示) 如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.
如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.