题目内容
10. 如图,菱形ABCD中,∠A=60°,边长为4,则它的对边所在直线之间的距离是( )
如图,菱形ABCD中,∠A=60°,边长为4,则它的对边所在直线之间的距离是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{4}{3}\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 直接利用菱形的性质结合锐角三角函数关系得出DE的长,进而得出答案.
解答  解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵菱形ABCD中,∠A=60°,边长为4,
∴AD=AB=4,
∴DE=sin60°×AD=2$\sqrt{3}$,
则它的对边所在直线之间的距离是2$\sqrt{3}$.
故选:B.
点评 此题主要考查了菱形的性质,正确应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
18.式子$\frac{3x}{2}$,$\frac{4}{x-y}$,x+y,$\frac{{{x^2}+1}}{π}$,$\frac{5b}{3a}$中是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.某校为了了解八年级学生身高情况,在全校范围内随机抽取了若干名学生进行调查,得到的数据如表:
(1)把身高按照150-155,155-160,160-165,165-170分组,数据包括右端点不包括左端点,写出众数所在的范围?
(2)请估计该校八年级学生的平均身高(精确到1cm)?
(3)请估计该校八年级学生的中等身高是多少cm?
(4)如果选出该校八年级学生中身高在155cm-160cm共60人组建体操表演队,则该队学生身高的波动水平(方差)是多少?
| 身高(cm) | 152 | 154 | 156 | 160 | 164 | 168 | 170 |
| 频数 | 1 | 1 | 2 | 6 | 4 | 4 | 2 |
(2)请估计该校八年级学生的平均身高(精确到1cm)?
(3)请估计该校八年级学生的中等身高是多少cm?
(4)如果选出该校八年级学生中身高在155cm-160cm共60人组建体操表演队,则该队学生身高的波动水平(方差)是多少?
 B.
B. 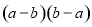
 D.
D. 
