题目内容
10.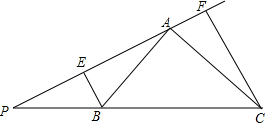 如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB.
分析 先征得△ABE≌△CAF,得到BE=AF,AE=CF,故EF=BE+CF,由∠FPC=30°,得到$\frac{1}{2}$PC=CF,$\frac{1}{2}$PB=BE,再根据线段的和差得到结论.
解答 证明:∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠EBA+∠BAE=∠BAE+∠CAF,
∴∠EBA=∠CAF;
在△ABE与△CAF中,
$\left\{\begin{array}{l}{∠ABE=∠FAC}\\{∠AEB=∠CFA}\\{AC=AB}\end{array}\right.$,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴EF=BE+CF,
∴CF=EF-BE,
∵∠FPC=30°,
$\frac{1}{2}PB=BE$,
$\frac{1}{2}$PC=CF=EF-BE,
$\frac{1}{2}$PB+$\frac{1}{2}$BC=EF-BE,
∴BE+$\frac{1}{2}$BC=EF-BE,
$\frac{1}{2}$BC=EF-2BE,
∴$\frac{1}{2}$BC=EF-PB.
点评 该题主要考查了全等三角形的判定及其性质的应用问题,含30°直角三角形的性质,解题的关键是深入观察图形结构特点,准确找出图形中隐含的相等或全等关系.

练习册系列答案
相关题目
2.若点B在直线AC上,AB=10,BC=5,则A、C两点间的距离是( )
| A. | 5 | B. | 15 | C. | 5或15 | D. | 不能确定 |
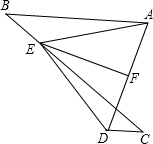 如图,已知AB∥CD,点E在BC上且BE=CD,AB=CE,EF平分∠AED.
如图,已知AB∥CD,点E在BC上且BE=CD,AB=CE,EF平分∠AED.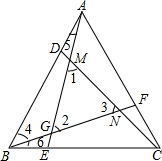 如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.
如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明. 如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.
如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.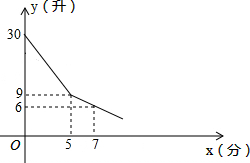 某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.
某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.