题目内容
若k=
=
=
(k≠0),则
的值为
| a+b |
| c |
| b+c |
| a |
| a+c |
| b |
| k2-4 |
| k2-4k+4 |
-
| 1 |
| 3 |
-
.| 1 |
| 3 |
分析:分①a+b+c=0时,求出k=-1,然后代入比例式进行计算即可得解;
②a+b+c=0时,根据合比性质求出k=2,然后代入比例式进行计算即可得解.
②a+b+c=0时,根据合比性质求出k=2,然后代入比例式进行计算即可得解.
解答:解:①a+b+c=0时,a+b=-c,
∴k=-1,
∴
=
=-
;
②a+b+c=0时,
∵k=
=
=
,
∴k=
=2,
当k=2时,k2-4k+4=0,
原始无意义,舍去.
故答案为:-
.
∴k=-1,
∴
| k2-4 |
| k2-4k+4 |
| (-1)2-4 |
| (-1)2-4×(-1)+4 |
| 1 |
| 3 |
②a+b+c=0时,
∵k=
| a+b |
| c |
| b+c |
| a |
| a+c |
| b |
∴k=
| 2(a+b+c) |
| a+b+c |
当k=2时,k2-4k+4=0,
原始无意义,舍去.
故答案为:-
| 1 |
| 3 |
点评:本题考查了比例的性质,主要利用了合比性质,熟记性质是解题的关键,难点在于要分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=
=
=t,则一次函数y=tx+t2的图象必定经过的象限是( )
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| A、第一、二象限 |
| B、第一、二、三象限 |
| C、第二、三、四象限 |
| D、第三、四象限 |
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若E为BC的中点,则tan∠CAE的值是
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,若E为BC的中点,则tan∠CAE的值是 (2012•随州)如图,直线l与反比例函数y=
(2012•随州)如图,直线l与反比例函数y=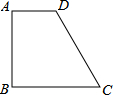 (2013•思明区一模)已知:四边形ABCD,AD∥BC,∠A=90°.
(2013•思明区一模)已知:四边形ABCD,AD∥BC,∠A=90°. 如图,已知梯形ABCD中,CD∥AB,M为腰AD上的一点,若AB+CD=BC,MC平分∠DCB.求证:BM⊥MC.
如图,已知梯形ABCD中,CD∥AB,M为腰AD上的一点,若AB+CD=BC,MC平分∠DCB.求证:BM⊥MC.