题目内容
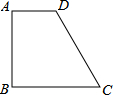（2013•思明区一模）已知：四边形ABCD，AD∥BC，∠A=90°．（1）若AD=BC，判断四边形ABCD的形状，并说明理由；
（2）如图，若AD＜BC，cos∠C=
| 3 | 5 |
分析：（1）根据平行线的判定得出四边形ABCD为平行四边形进而利用矩形的判定得出即可；
（2）利用锐角三角函数的关系得出cos∠C=
，得出
=
，即
=
，即可得出y与x的函数关系，进而画出图象．
（2）利用锐角三角函数的关系得出cos∠C=
| 3 |
| 5 |
| EC |
| DC |
| 3 |
| 5 |
| y-x |
| x+y |
| 3 |
| 5 |
解答：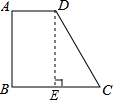
解：（1）四边形ABCD为矩形，
∵AD∥BC，AD=BC，
∴四边形ABCD为平行四边形，
又∵∠A=90°，
∴四边形ABCD是矩形．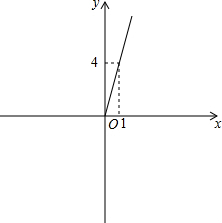
（2）如图，过点D作DE⊥BC于点E，
∵AD=x，BC=y，DC=AD+BC，
∴EC=y-x，DC=x+y．
在Rt△DEC中，∠DEC=90°，cos∠C=
，
∴
=
，即
=
，
∴y=4x（x＞0）
如图所示：
解：（1）四边形ABCD为矩形，∵AD∥BC，AD=BC，
∴四边形ABCD为平行四边形，
又∵∠A=90°，
∴四边形ABCD是矩形．
（2）如图，过点D作DE⊥BC于点E，
∵AD=x，BC=y，DC=AD+BC，
∴EC=y-x，DC=x+y．
在Rt△DEC中，∠DEC=90°，cos∠C=
| 3 |
| 5 |
∴
| EC |
| DC |
| 3 |
| 5 |
| y-x |
| x+y |
| 3 |
| 5 |
∴y=4x（x＞0）
如图所示：
点评：此题主要考查了平行线的判定以及矩形的判定和锐角三角函数的关系等知识，根据已知得出
=
是解题关键．
| EC |
| DC |
| 3 |
| 5 |
练习册系列答案
相关题目
（2013•思明区一模）如图，△ABC中，点D在BC的延长线上，若∠ACD=100°，∠A=40°，则∠B的度数是（ ）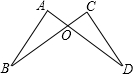
（2013•思明区一模）如图，AD与BC相交于点O，∠A=∠C，添加一个条件