题目内容
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=36°,求∠BED的度数;
(2)作出△BED中DE边上的高,垂足为H;
(3)若△ABC面积为20,过点C作CF∥AD交BA的延长线于点F,求△BCF的面积.(友情提示:两条平行线间的距离处处相等.)
考点:作图—复杂作图,平行线之间的距离
专题:
分析:(1)利用三角形的外角定理直接求出即可;
(2)延长ED,进而过点B作BH⊥AD即可;
(3)利用两条平行线间的距离处处相等得出S△AFC=S△DFC.而S△DFC=
S△BCF,故S△AFC=
S△BCF,求出即可.
(2)延长ED,进而过点B作BH⊥AD即可;
(3)利用两条平行线间的距离处处相等得出S△AFC=S△DFC.而S△DFC=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)∵∠ABE=15°,∠BAD=36°,
解:(1)∵∠ABE=15°,∠BAD=36°,
∴∠BED=∠ABE+∠BAD=51°;
(2)如图所示:BH即为所求;
(3)过点C作CF∥AD交BA的延长线于点F,
∵AD∥CF,
∴S△AFC=S△DFC.
而S△DFC=
S△BCF,∴S△AFC=
S△BCF.
∴S△AFC=S△ABC=20,∴S△BCF=40.
 解:(1)∵∠ABE=15°,∠BAD=36°,
解:(1)∵∠ABE=15°,∠BAD=36°,∴∠BED=∠ABE+∠BAD=51°;
(2)如图所示:BH即为所求;
(3)过点C作CF∥AD交BA的延长线于点F,
∵AD∥CF,
∴S△AFC=S△DFC.
而S△DFC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AFC=S△ABC=20,∴S△BCF=40.
点评:此题主要考查了三角形外角的性质以及三角形高的做法和平行线的性质等知识,得出S△AFC=
S△BCF是解题关键.
| 1 |
| 2 |

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
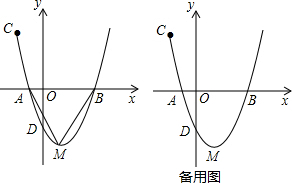 如图,已知二次函数y=x2+bx+c的图象经过两点C(-2,5)与D(0,-3),且与x轴相交于A、B两点,其顶点为M.
如图,已知二次函数y=x2+bx+c的图象经过两点C(-2,5)与D(0,-3),且与x轴相交于A、B两点,其顶点为M.
