题目内容
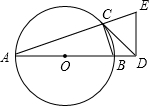 已知如图,D是⊙O的直径AB延长线上一点,DC切⊙O于C,过D作ED⊥AD与AC的延长线相交于E.
已知如图,D是⊙O的直径AB延长线上一点,DC切⊙O于C,过D作ED⊥AD与AC的延长线相交于E.(1)求证:CD=DE;
(2)若tan∠BAC=
| 1 |
| 3 |
| CE |
| AC |
(3)设AB=2R,当BC=CE时,求BD的长.
分析:(1)欲求CD=DE,需先求出∠DCE=∠E;由弦切角定理知∠DCB=∠A;可发现:∠DCE和∠E是上面证得的两个等角的余角,故∠DCE=∠E,由此得证.
(2)设出BC=x,ED=y;根据tan∠BAC=
,得出AD=3x,AC=3y,根据勾股定理和切割线定理即可求出x和y之间的关系.
(3)连接OC,由(1)得出的∠BCD=∠A,易知:∠OBC=∠CDE,因此等腰△OBC和等腰△DCE相似;由于题中告诉了BC=CE,可得到的条件是△OBC≌△DCE;因此OC=CD=R;在等腰Rt△OCD中,已知了直角边的长,即可求出斜边OD的长,进而可求出BD的长.
(2)设出BC=x,ED=y;根据tan∠BAC=
| 1 |
| 3 |
(3)连接OC,由(1)得出的∠BCD=∠A,易知:∠OBC=∠CDE,因此等腰△OBC和等腰△DCE相似;由于题中告诉了BC=CE,可得到的条件是△OBC≌△DCE;因此OC=CD=R;在等腰Rt△OCD中,已知了直角边的长,即可求出斜边OD的长,进而可求出BD的长.
解答:(1)证明:∵△ADE是直角三角形,
∴∠E=90°-∠A;
又∵∠BCD=∠A,∠BCE=90°,
∴∠DCE=90°-∠A,
∴∠E=∠DCE,即CD=DE.
(2)解:设BC=y,ED=x;根据tan∠BAC=
,得出AD=3x,AC=3y;
Rt△ABC中,根据勾股定理,得:AB=
=
y;
又因为CD=DE,所以根据切割线定理,x2=BD•3x,BD=
,AB=3x-
=
x;
所以
y=
x,
=
.
又因为
=
=
-1=
×
-1=
.
(3)解:连接OC;
由(1)知:∠BCD=∠A,∠ACB=∠BCE=90°;
∴∠OBC=∠DCE;
∵OB=OC,CD=DE;
∴∠OBC=∠OCB=∠DCE=∠E;
在△OBC和△DCE中
∴△OBC≌△DCE(ASA);
∴OC=CD=R;
Rt△OCD中,OC=CD=R,∠OCD=90°;
∴OD=
R,即BD=OD-OB=(
-1)R.
∴∠E=90°-∠A;
又∵∠BCD=∠A,∠BCE=90°,
∴∠DCE=90°-∠A,
∴∠E=∠DCE,即CD=DE.
(2)解:设BC=y,ED=x;根据tan∠BAC=
| 1 |
| 3 |
Rt△ABC中,根据勾股定理,得:AB=
| (3y)2+y2 |
| 10 |
又因为CD=DE,所以根据切割线定理,x2=BD•3x,BD=
| x |
| 3 |
| x |
| 3 |
| 8 |
| 3 |
所以
| 10 |
| 8 |
| 3 |
| x |
| y |
3
| ||
| 8 |
又因为
| CE |
| AC |
| ||
| 3y |
| ||
| 3 |
| x |
| y |
| ||
| 3 |
3
| ||
| 8 |
| 1 |
| 4 |
(3)解:连接OC;

由(1)知:∠BCD=∠A,∠ACB=∠BCE=90°;
∴∠OBC=∠DCE;
∵OB=OC,CD=DE;
∴∠OBC=∠OCB=∠DCE=∠E;
在△OBC和△DCE中
|
∴△OBC≌△DCE(ASA);
∴OC=CD=R;
Rt△OCD中,OC=CD=R,∠OCD=90°;
∴OD=
| 2 |
| 2 |
点评:此题巧妙利用了勾股定理、切割线弦定及三角函数值,将各个量结合起来,找到它们之间的关系,尤其是(2),借助参数求代数式的比,应用了设而不求的方法.

练习册系列答案
相关题目
 23、已知如图,C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
23、已知如图,C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.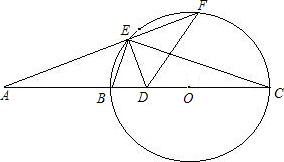 已知如图,A是⊙O的直径CB延长线上一点,BC=2AB,割线AF交⊙O于E、F,D是OB的中点,且DE⊥AF,连接BE、DF.
已知如图,A是⊙O的直径CB延长线上一点,BC=2AB,割线AF交⊙O于E、F,D是OB的中点,且DE⊥AF,连接BE、DF.
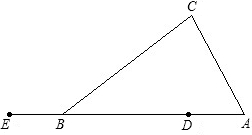
 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)