Question

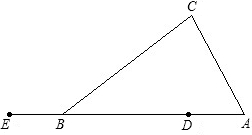
已知如图，D是△ABC的AB边上一点，E在AB的延长线上．
（1）作射线ET，使∠AET=∠CAB（保留作图痕迹，不写作法）
（2）在射线ET上取一点F，使EF=AC，连接DF，试证明当AD=EB时，BC=DF．

Answer 1

分析：（1）根据作一个角等于已知角的作法画图即可；
（2）利用SAS定理证明△FED≌△CAB，可以得到BC=DF．

解答：解：（1）如图所示


（2）∵AD=EB，
∴AD+BD=EB+BD，
即：ED=AB，
在△FED和△CAB中

EF=AC ∠A=∠E ED=AB

，
∴△FED≌△CAB，
∴CB=DF．

点评：此题主要考查了作一个角等于已知角，三角形全等的判定以及性质，关键是根据题意画出图形，再证明△FED≌△CAB．