题目内容
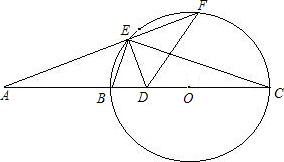 已知如图,A是⊙O的直径CB延长线上一点,BC=2AB,割线AF交⊙O于E、F,D是OB的中点,且DE⊥AF,连接BE、DF.
已知如图,A是⊙O的直径CB延长线上一点,BC=2AB,割线AF交⊙O于E、F,D是OB的中点,且DE⊥AF,连接BE、DF.(1)试判断BE与DF是否平行?请说明理由;
(2)求AE:EC的值.
分析:(1)一般判断的结论大多数是肯定的,但这个是否定的.如图过O作OM⊥EF,垂足为M,则EM=MF,容易知道DE∥OM,根据平行线分线段成比例可以求出AE:AF=3:5,不等于AB:AD,所以BE与DF不平行;
(2)要求AE:EC,不能直接求出.由于D是AC的中点,取AE的中点,利用中位线定理进行转换,连接DP.根据已知条件和平行线分线段成比例可以证明△EDP是等腰直角三角形,再利用等腰直角三角形的性质即可求出AE:EC.
(2)要求AE:EC,不能直接求出.由于D是AC的中点,取AE的中点,利用中位线定理进行转换,连接DP.根据已知条件和平行线分线段成比例可以证明△EDP是等腰直角三角形,再利用等腰直角三角形的性质即可求出AE:EC.
解答: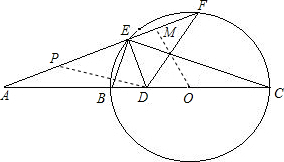 解:(1)BE与DF不平行(1分)
解:(1)BE与DF不平行(1分)
理由:过O作OM⊥EF,垂足为M,则EM=MF
∵DE⊥AE,∴DE∥OM
∴AE:AM=AD:AO=3:4 (1分)
∴AE:AF=3:5
∵AB:AD=2:3
∴AE:AF≠AB:AD
∴BE与DF不平行;
(2)取AE的中点P,连接DP交BE于Q
∵D是AC的中点,P是AE的中点
∴DP∥CE
∵BE⊥EC,∴BE⊥DQ
由DQ∥CE,得
=
=
,又
=
∴DP=2DQ即DQ=PQ,又BE⊥DP
∴BE是DP的中垂线
∴EP=ED (2分)
∵∠AED=90°,
∴△EDP是等腰直角三角形
∴DP=
EP
∴AE:EC=2EP:2DP=1:
.(1分)
 解:(1)BE与DF不平行(1分)
解:(1)BE与DF不平行(1分)理由:过O作OM⊥EF,垂足为M,则EM=MF
∵DE⊥AE,∴DE∥OM
∴AE:AM=AD:AO=3:4 (1分)
∴AE:AF=3:5
∵AB:AD=2:3
∴AE:AF≠AB:AD
∴BE与DF不平行;
(2)取AE的中点P,连接DP交BE于Q
∵D是AC的中点,P是AE的中点
∴DP∥CE
∵BE⊥EC,∴BE⊥DQ
由DQ∥CE,得
| DQ |
| CE |
| BD |
| BC |
| 1 |
| 4 |
| DP |
| CE |
| 1 |
| 2 |
∴DP=2DQ即DQ=PQ,又BE⊥DP
∴BE是DP的中垂线
∴EP=ED (2分)
∵∠AED=90°,
∴△EDP是等腰直角三角形
∴DP=
| 2 |
∴AE:EC=2EP:2DP=1:
| 2 |
点评:此题比较难,主要利用平行线分线段成比例和中位线定理解题,也结合了等腰直角三角形的性质来求出比值.

练习册系列答案
相关题目
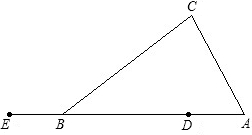
 23、已知如图,C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
23、已知如图,C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)