题目内容
 已知:如图,等边△ABC中,D为AC的中点,DG∥BG交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于F点.
已知:如图,等边△ABC中,D为AC的中点,DG∥BG交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于F点.(1)求证:△CDE≌△GDF;
(2)求证:AF-CE=
| 1 |
| 2 |
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据等边三角形的性质得出AB=AC=BC,∠A=∠B=∠ACB=60°,求出DG=DC,∠GDF=∠CDE,根据ASA推出△DCE≌△DGF即可;
(2)根据全等三角形的性质得出CE=GF,即可得出答案.
(2)根据全等三角形的性质得出CE=GF,即可得出答案.
解答:证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠A=∠B=∠ACB=60°,
∵D为AC的中点,
∴AD=DC=
AC,
∵DG∥BC,
∴∠AGD=∠B=∠ADG=∠C=60°,
∴△ADG为等边三角形.
∴AG=DG=AD,
∴DG=DC,
∵∠EDF=∠GDC=120°,
∴∠GDF=∠CDE,
在△DCE和△DGF中
∴△DCE≌△DGF;
(2)∵△DCE≌△DGF,
∴CE=GF,
∴AF-CE=AF-GF=AG=
AB.
∴AB=AC=BC,∠A=∠B=∠ACB=60°,
∵D为AC的中点,
∴AD=DC=
| 1 |
| 2 |
∵DG∥BC,
∴∠AGD=∠B=∠ADG=∠C=60°,
∴△ADG为等边三角形.
∴AG=DG=AD,
∴DG=DC,
∵∠EDF=∠GDC=120°,
∴∠GDF=∠CDE,
在△DCE和△DGF中
|
∴△DCE≌△DGF;
(2)∵△DCE≌△DGF,
∴CE=GF,
∴AF-CE=AF-GF=AG=
| 1 |
| 2 |
点评:本题考查了等边三角形的,全等三角形的性质和判定的应用,解此题的关键是求出△DCE≌△DGF,注意:等边三角形的三边都相等,等边三角形的每个角都等于60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在
、-
、
、
这四个数中,无理数有( )
| 22 |
| 7 |
| 2 |
| 3 | 27 |
| π |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
数轴上的点A到原点的距离是8,则点A表示的数为( )
| A、8 | B、4或-4 |
| C、8或-8 | D、4 |
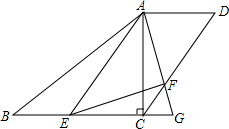 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.


