题目内容
19.直角三角形一边长为12,另两边的长度是方程x2-18x+a=0的两根,求a的值.分析 分两种情况:①设另一条直角边长为b,斜边长为c,由根与系数的关系得出c+b=18,bc=a,由勾股定理和完全平方公式得出a的方程,解方程即可;
②设一条直角边长为b,另一条直角边长为c,由根与系数的关系得出c+b=18,bc=a,由勾股定理和完全平方公式得出a的方程,解方程即可.
解答 解:分两种情况:
①设另一条直角边长为b,斜边长为c,
由根与系数的关系得:c+b=18,bc=a,
∴(c-b)2=(c+b)2-4bc=182-4a,
∴$\sqrt{c-b}=\sqrt{1{8}^{2}-4a}$,
由勾股定理得:c2-b2=122,
∴(c+b)(c-b)=122,
∴18$\sqrt{1{8}^{2}-4a}$=122,
解得:a=65;
②设一条直角边长为b,另一条直角边长为c,
由根与系数的关系得:c+b=18,bc=a,
∴b2+c2=(b+c)2-2bc=182-2a,
由勾股定理得:c2+b2=122,
∴182-2a=122,
解得:a=90;
所以a=65或a=90.
点评 本题考查了根与系数的关系、勾股定理、完全平方公式;熟练掌握根与系数的关系,由勾股定理和完全平方公式得出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若方程4x2-(m-2)x+1=0的左边可以写成一个完全平方式,则m的值为( )
| A. | -2 | B. | -2或6 | C. | -2或-6 | D. | 2或-6 |
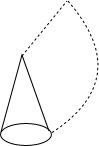 (1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;
(1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;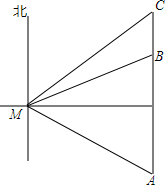 如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.
如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时. 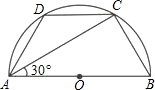 如图,已知在半圆AOB中,AD=DC,∠CAB=30°,AB=8,求AD的长.
如图,已知在半圆AOB中,AD=DC,∠CAB=30°,AB=8,求AD的长.