题目内容
在正方形网格如图:(每一个小正方形边长为1)中,画一个△ABC,使AB、BC、AC的三边长分别为| 5 |
| 10 |
| 13 |
(1)写出△ABC的面积为
(2)求△ABC中,AC边上的高为

分析:根据题意,由勾股定理可以作图,
(1)分析图形可得,S△ABC=S正方形NMCH-S△ABN-S△AMC-S△BHC,计算可得答案,
(2)由(1)的结论,又由AC=
,由三角形的面积公式,计算可得答案.
(1)分析图形可得,S△ABC=S正方形NMCH-S△ABN-S△AMC-S△BHC,计算可得答案,
(2)由(1)的结论,又由AC=
| 13 |
解答:解:根据题意,由勾股定理作图可得,

(1)易得S△ABC=S正方形NMCH-S△ABN-S△AMC-S△BHC=
3×3-
×2×1-
×2×3-
×1×3=
,
(2)由(1)的结论,S△ABC=
,
又由AC=
,
则AC边上的高为
=
;
答:三角形ABC的面积为
,AC边上的高为
.

(1)易得S△ABC=S正方形NMCH-S△ABN-S△AMC-S△BHC=
3×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
(2)由(1)的结论,S△ABC=
| 7 |
| 2 |
又由AC=
| 13 |
则AC边上的高为
2×
| ||
|
7
| ||
| 13 |
答:三角形ABC的面积为
| 7 |
| 2 |
7
| ||
| 13 |
点评:本题考查了学生作图与根据图象分析处理、以及分割图形计算面积的能力.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 (2013•石景山区一模)如图,在正方形网格(图中每个小正方形的边长均为1)中,一段圆弧经过网格的格点A、B、C.则弧AC所在圆的半径长为
(2013•石景山区一模)如图,在正方形网格(图中每个小正方形的边长均为1)中,一段圆弧经过网格的格点A、B、C.则弧AC所在圆的半径长为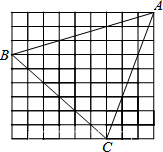 如图,在正方形网格(图中每个小正方形的边长均为1)中,△ABC的三个顶点均在格点上,则△ABC的周长为
如图,在正方形网格(图中每个小正方形的边长均为1)中,△ABC的三个顶点均在格点上,则△ABC的周长为 、
、 、
、 .
.
 如图,在正方形网格(图中每个小正方形的边长均为1)中,一段圆弧经过网格的格点A、B、C.则弧AC所在圆的半径长为________;弧AC的长为________.
如图,在正方形网格(图中每个小正方形的边长均为1)中,一段圆弧经过网格的格点A、B、C.则弧AC所在圆的半径长为________;弧AC的长为________.