Question

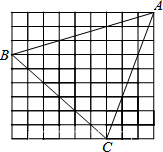如图，在正方形网格（图中每个小正方形的边长均为1）中，△ABC的三个顶点均在格点上，则△ABC的周长为

=6

2

+6

10

，面积为

36

．

Answer 1

分析：（1）根据勾股定理分别求出AB，BC，AC的长，从而求出△ABC的周长；
（2）三角形的面积等于正方形的面积减去△ABC之外的三个三角形的面积．

解答：解：由勾股定理得：AB=

32+92

=3

10

，
BC=

62+62

=6

2

，AC=

32+92

=3

10

，
所以△ABC的周长为AB+AC+BC=6

2

+6

10

，
S_△ABC=9×9-

1

2

×6×6-2×

1

2

×3×9=36，
故答案为：6

2

+6

10

，36．

点评：本题主要考查图象识别，从图象中分析出面积的计算，题目得以解决；另外，勾股定理也是考查点之一．