题目内容
如图，AB切⊙O于点B，∠A=30°，AB=
，则半径OB的长为
- A.1
- B.
- C.2
- D.4
C
分析：由于直线AB与⊙O相切于点B，则∠OBA=90°，AB=2，∠A=30°，根据三角函数定义即可求出OB．
解答：∵直线AB与⊙O相切于点A，
则∠OBA=90°．
∵AB=2，
∴tanA=
=
，
∴OB=2×=2．
故选C．
点评：本题主要利用了切线的性质和锐角三角函数的概念解直角三角形问题．
分析：由于直线AB与⊙O相切于点B，则∠OBA=90°，AB=2
，∠A=30°，根据三角函数定义即可求出OB．解答：∵直线AB与⊙O相切于点A，
则∠OBA=90°．
∵AB=2
，∴tanA=
=，∴OB=2
×=2．故选C．
点评：本题主要利用了切线的性质和锐角三角函数的概念解直角三角形问题．
练习册系列答案
相关题目
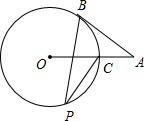已知：如图，AB切⊙O于点B，OA与⊙O交于点C，点P在⊙O上，若∠BAC=40°，则∠BPC的度数为（ ）| A、20° | B、25° | C、30° | D、40° |
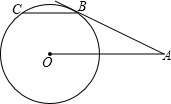如图，AB切⊙O于点B，OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
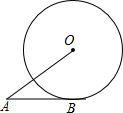如图，AB切⊙O于点B，AB=4cm，AO=6cm，则⊙O的半径为
（2012•西藏）如图，AB切⊙O于点B，延长AO交⊙O于点C，连接BC．若∠A=40°，则∠C=（ ）
（2012•广东模拟）如图，AB切⊙O于点A，OD⊥弦AC于点D，延长OD，交AB于点B，若∠O=60°，AC=6cm，则AB=