题目内容
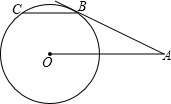 如图,AB切⊙O于点B,OA=2
如图,AB切⊙O于点B,OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
分析:连OB,OC,由AB切⊙O于点B,根据切线的性质得到OB⊥AB,在Rt△OBA中,OA=2
,AB=3,利用三角函数求出∠BOA=60°,同时得到OB=
OA=
,又根据平行线的性质得到∠BOA=∠CBO=60°,于是有∠BOC=60°,最后根据弧长公式计算出劣弧BC的长.
| 3 |
| 1 |
| 2 |
| 3 |
解答: 解:连OB,OC,如图,
解:连OB,OC,如图,
∵AB切⊙O于点B,
∴OB⊥AB,
在Rt△OBA中,OA=2
,AB=3,
sin∠BOA=
=
=
,
∴∠BOA=60°,
∴OB=
OA=
,
又∵弦BC∥OA,
∴∠BOA=∠CBO=60°,
∴△OBC为等边三角形,即∠BOC=60°,
∴劣弧BC的弧长=
=
.
故选A.
 解:连OB,OC,如图,
解:连OB,OC,如图,∵AB切⊙O于点B,
∴OB⊥AB,
在Rt△OBA中,OA=2
| 3 |
sin∠BOA=
| AB |
| OA |
| 3 | ||
2
|
| ||
| 2 |
∴∠BOA=60°,
∴OB=
| 1 |
| 2 |
| 3 |
又∵弦BC∥OA,
∴∠BOA=∠CBO=60°,
∴△OBC为等边三角形,即∠BOC=60°,
∴劣弧BC的弧长=
60•π•
| ||
| 180 |
| ||
| 3 |
故选A.
点评:本题考查了弧长公式:l=
.也考查了切线的性质和特殊角的三角函数值.
| n•π•R |
| 180 |

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
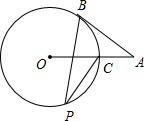 已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )
已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )| A、20° | B、25° | C、30° | D、40° |
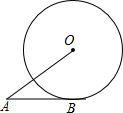 如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为
如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为 (2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )
(2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( ) (2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=
(2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=