题目内容
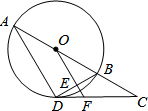 (2013•门头沟区二模)如图,AB是⊙O的直径,C是AB延长线上一点,点D在⊙O上,且∠A=30°,∠ABD=2∠BDC.
(2013•门头沟区二模)如图,AB是⊙O的直径,C是AB延长线上一点,点D在⊙O上,且∠A=30°,∠ABD=2∠BDC.(1)求证:CD是⊙O的切线;
(2)过点O作OF∥AD,分别交BD、CD于点E、F.若OB=2,求OE和CF的长.
分析:(1)首先连接OD,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ADB=90°,又由∠A=30°,∠ABD=2∠BDC,易证得△ODB是等边三角形,继而求得∠ODC=90°,即CD是⊙O的切线;
(2)由三角函数的性质,即可求得CD与DF的长,继而求得答案.
(2)由三角函数的性质,即可求得CD与DF的长,继而求得答案.
解答: (1)证明:连结OD.
(1)证明:连结OD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠A=30°,
∴∠ABD=60°.
∵∠ABD=2∠BDC,
∴∠BDC=
∠ABD=30°.
∵OD=OB,
∴△ODB是等边三角形.
∴∠ODB=60°.
∴∠ODC=∠ODB+∠BDC=90°.
∴CD是⊙O的切线.
(2)解:∵OF∥AD,∠ADB=90°,
∴OF⊥BD,∠BOE=∠A=30°. …(3分)
∵BD=OB=2,
∴DE=BE=
BD=1.
∴OE=
=
.
∵OD=OB=2,∠DOC=60°,∠DOF=30°,
∴CD=OD•tan60°=2
,DF=OD•tan30°=
.
∴CF=CD-DF=2
-
=
.
 (1)证明:连结OD.
(1)证明:连结OD.∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠A=30°,
∴∠ABD=60°.
∵∠ABD=2∠BDC,
∴∠BDC=
| 1 |
| 2 |
∵OD=OB,
∴△ODB是等边三角形.
∴∠ODB=60°.
∴∠ODC=∠ODB+∠BDC=90°.
∴CD是⊙O的切线.
(2)解:∵OF∥AD,∠ADB=90°,
∴OF⊥BD,∠BOE=∠A=30°. …(3分)
∵BD=OB=2,
∴DE=BE=
| 1 |
| 2 |
∴OE=
| OB2-BE2 |
| 3 |
∵OD=OB=2,∠DOC=60°,∠DOF=30°,
∴CD=OD•tan60°=2
| 3 |
| 2 |
| 3 |
| 3 |
∴CF=CD-DF=2
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
点评:此题考查了切线的判定、等边三角形的判定与性质、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
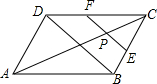 (2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( ) (2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是
(2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是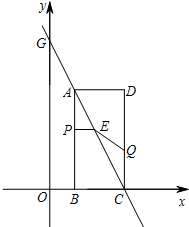 (2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.
(2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.