题目内容
14.8的算术平方根是2$\sqrt{2}$;8的立方根是2.分析 依据算术平方根的性质和立方根的性质解答即可.
解答 解:8的算术平方根是2$\sqrt{2}$;8的立方根是2.
故答案为:2$\sqrt{2}$;2.
点评 本题主要考查的是算术平方根、立方根的性质,熟练掌握算术平方根、立方根的性质是解题的关键.

练习册系列答案
相关题目
5.下列各数中,属于无理数的是( )
| A. | $\sqrt{4}$ | B. | -2 | C. | π | D. | 0 |
2.估计$\sqrt{41}$-2的值( )
| A. | 在4和5之间 | B. | 在3和4之间 | C. | 在2和3之间 | D. | 在1和2之间 |
19.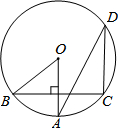 如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )
如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )
 如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )
如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,∠ADC=26°,那么∠AOB的度数为( )| A. | 64° | B. | 26° | C. | 52° | D. | 38° |
6. 如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )
如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )
 如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )
如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
3.在-4,2,-1,$\sqrt{3}$这四个数中,最小的数是( )
| A. | -1 | B. | 2 | C. | $\sqrt{3}$ | D. | -4 |
7.四个数$\sqrt{2-\sqrt{3}}$,$\sqrt{2-\sqrt{2-\sqrt{3}}}$,$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{3}}}}$,$\sqrt{2+\sqrt{2-\sqrt{2-\sqrt{3}}}}$的乘积为( )
| A. | 2+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | 2-$\sqrt{3}$ |




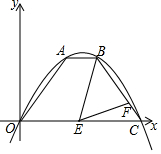 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.